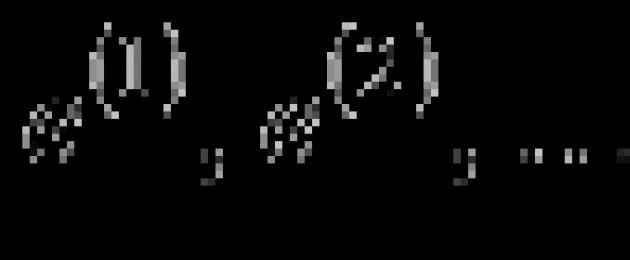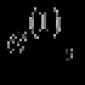Знайти базис та розмірність лінійних підпросторів. Розмірність та базис векторного простору, розкладання вектора за базисом, приклади. Приклади базисів лінійних просторів

Коли ми розбирали поняття n-мірного вектора та вводили операції над векторами, то з'ясували, що безліч усіх n-мірних векторів породжує лінійний простір. У цій статті ми поговоримо про найважливіші пов'язані поняття – розмірність і базис векторного простору. Також розглянемо теорему про розкладання довільного вектора за базисом і зв'язок між різними базисами n-мірного простору. Докладно розберемо рішення характерних прикладів.

Навігація на сторінці.

Концепція розмірності векторного простору та базису.

Поняття розмірності та базису векторного простору безпосередньо пов'язані з поняттям лінійно незалежної системи векторів, тому рекомендуємо при необхідності звертатися до статті лінійна залежність системи векторів, властивості лінійної залежності та незалежності.

Визначення.

Розмірність векторного просторуназивається число, що дорівнює максимальній кількості лінійно незалежних векторів у цьому просторі.

Визначення.

Базис векторного простору– це впорядкована сукупність лінійно незалежних векторів цього простору, число яких дорівнює розмірності простору.

Наведемо деякі міркування, виходячи з цих визначеннях.

Розглянемо простір n-мірних векторів.

Покажемо, що розмірність цього простору дорівнює n.

Візьмемо систему з n одиничних векторів виду

Приймемо ці вектори як рядки матриці А . І тут матриця А буде одиничною матрицею розмірності n на n . Ранг цієї матриці дорівнює n (за необхідності дивіться статтю). Отже, система векторів лінійно незалежна, причому до цієї системи не можна додати жодного вектора, не порушивши її лінійної незалежності. Оскільки число векторів у системі одно n , то розмірність простору n-мірних векторів дорівнює n, а одиничні вектори є базисом цього простору.

З останнього затвердження та визначення базису можна зробити висновок, що будь-яка система n-мірних векторів, число векторів у якій менше n, не є базисом.

Тепер переставимо місцями перший та другий вектор системи . Легко показати, що отримана система векторів також є базисом n-мірного векторного простору. Складемо матрицю, прийнявши її рядками вектори системи. Ця матриця може бути отримана з одиничної матриці перестановкою місцями першого і другого рядків, отже, її ранг дорівнюватиме n . Таким чином, система з n векторів лінійно незалежна і є базисом n-мірного векторного простору.

Якщо переставити місцями інші вектори системи , то отримаємо ще один базис.

Якщо взяти лінійно незалежну систему не одиничних векторів, вона також є базисом n -мірного векторного простору.

Таким чином, Векторний простір розмірності n має стільки базисів, скільки існує лінійно незалежних систем з n n -мірних векторів.

Якщо говорити про двовимірний векторний простір (тобто, про площину), то її базисом є два будь-які не колінеарні вектори. Базисом тривимірного простору є три будь-які некомпланарні вектори.

Розглянемо кілька прикладів.

приклад.

Чи є вектори базисом тривимірного простору?

Рішення.

Досліджуємо цю систему векторів на лінійну залежність. Для цього складемо матрицю, рядками якої будуть координати векторів, і знайдемо її ранг:


Таким чином, вектори a, b і c лінійно незалежні та їх кількість дорівнює розмірності векторного простору, отже вони є базисом цього простору.

Відповідь:

Так, є.

приклад.

Чи може бути векторна система базисом векторного простору?

Рішення.

Ця система векторів лінійно залежна, оскільки максимальне число лінійно незалежних тривимірних векторів дорівнює трьом. Отже, ця система векторів може бути базисом тривимірного векторного простору (хоча підсистема вихідної системи векторів є базисом).

Відповідь:

Ні не може.

приклад.

Переконайтеся, що вектори

може бути базисом чотиривимірного векторного простору.

Рішення.

Складемо матрицю, прийнявши її рядками вихідні вектори:

Знайдемо:

Таким чином, система векторів a, b, c, d лінійно незалежна та їх кількість дорівнює розмірності векторного простору, отже, a, b, c, d є його базисом.

Відповідь:

Вихідні вектори є базисом чотиривимірного простору.

приклад.

Чи становлять вектори базис векторного простору розмірності 4?

Рішення.

Навіть якщо вихідна система векторів лінійно незалежна, кількість векторів у ній недостатньо для того, щоб бути базисом чотиривимірного простору (бази такого простору складається з 4 векторів).

Відповідь:

Ні, не складає.

Розкладання вектора за базисом векторного простору.

Нехай довільні вектори є базисом n-вимірного векторного простору. Якщо до них додати деякий n-вимірний вектор x, то отримана система векторів буде лінійно залежною. З властивостей лінійної залежності ми знаємо, що хоча б один вектор лінійно-залежної системи лінійно виражається через інші. Іншими словами, хоча б один із векторів лінійно залежної системи розкладається за іншими векторами.

Так ми наблизилися до дуже важливої ​​теореми.

Теорема.

Будь-який вектор n-вимірного векторного простору єдиним чином розкладається по базису.

Доведення.

Нехай - Базис n-мірного векторного простору. Додамо до цих векторів n-мірний вектор x. Тоді отримана система векторів буде лінійно залежною та вектор x може бути лінійно виражений через вектори : де - деякі числа. Так ми отримали розкладання вектора x базисом. Залишилося довести, що це розкладання єдине.

Припустимо, що існує ще одне розкладання, де - Деякі числа. Віднімемо від лівої та правої частин останньої рівності відповідно ліву та праву частини рівності:

Оскільки система базисних векторів лінійно незалежна, то за визначенням лінійної незалежності системи векторів отримана рівність можлива лише тоді, коли всі коефіцієнти дорівнюють нулю. Тому, що доводить єдиність розкладання вектора по базису.

Визначення.

Коефіцієнти називаються координатами вектора x у базисі .

Після знайомства з теоремою про розкладання вектора по базису, ми починаємо розуміти суть виразу «нам заданий n-мірний вектор ». Це означає, що ми розглядаємо вектор x n -мірного векторного простору, координати якого задані в деякому базисі. При цьому ми розуміємо, що цей вектор x в іншому базисі n-мірного векторного простору буде мати координати, відмінні від .

Розглянемо таку задачу.

Нехай у деякому базисі n-мірного векторного простору нам задана система з n лінійно незалежних векторів

та вектор . Тоді вектори є також базисом цього векторного простору.

Нехай нам потрібно знайти координати вектора x у базисі . Позначимо ці координати як .

Вектор x у базисі має уявлення. Запишемо цю рівність у координатній формі:

Ця рівність рівносильна системі з n лінійних рівнянь алгебри з n невідомими змінними :

Основна матриця цієї системи має вигляд

Позначимо її літерою А. Стовпці матриці А є векторами лінійно незалежної системи векторів. тому ранг цієї матриці дорівнює n , отже, її визначник відмінний від нуля. Цей факт вказує на те, що система рівнянь має єдине рішення, яке може бути знайдено будь-яким методом, наприклад, або .

Так буде знайдено шукані координати вектора x у базисі .

Розберемо теорію з прикладів.

приклад.

В деякому базисі тривимірного векторного простору задані вектори

Переконайтеся, що система векторів також є базисом цього простору та знайдіть координати вектора x у цьому базисі.

Рішення.

Щоб система векторів була базисом тривимірного простору, потрібно, щоб вона була лінійно незалежна. З'ясуємо це, визначивши ранг матриці A рядками якої є вектори . Ранг знайдемо методом Гауса


отже, Rank(A) = 3 що показує лінійну незалежність системи векторів .

Отже, вектори є базисом. Нехай у цьому базисі вектор x має координати. Тоді, як ми показали вище, зв'язок координат цього вектора задається системою рівнянь

Підставивши до неї відомі з умови значення, отримаємо

Вирішимо її методом Крамера:

Таким чином, вектор x у базисі має координати .

Відповідь:

приклад.

У деякому базисі чотиривимірного векторного простору задана лінійно незалежна система векторів

Відомо що . Знайдіть координати вектора x у базисі .

Рішення.

Оскільки система векторів лінійно незалежна за умовою, вона є базисом чотиривимірного простору. Тоді рівність означає, що вектор x у базисі має координати. Позначимо координати вектора x у базисі як .

Система рівнянь, що задає зв'язок координат вектора x у базисах і має вид

Підставляємо в неї відомі значення і знаходимо шукані координати:

Відповідь:

.

Зв'язок між базисами.

Нехай у деякому базисі n-мірного векторного простору задані дві лінійно незалежні системи векторів

і

тобто, вони також є базисами цього простору.

Якщо - координати вектора у базисі , то зв'язок координат і задається системою лінійних рівнянь (про це ми говорили у попередньому пункті):

, яка в матричній формі може бути записана як

Аналогічно для вектора, ми можемо записати

Попередні матричні рівності можна об'єднати в одну, яка, по суті, задає зв'язок векторів двох різних базисів.

Аналогічно ми можемо висловити всі вектори базису через базис :

Визначення.

Матрицю називають матрицею переходу від базису до базису тоді справедлива рівність

Помноживши обидві частини цієї рівності праворуч

отримаємо

Знайдемо матрицю переходу, при цьому не будемо докладно зупинятись на знаходженні зворотної матриці та множенні матриць (дивіться при необхідності статті та ):

Залишилося з'ясувати зв'язок координат вектора в заданих базисах.

Нехай у базисі вектор x має координати, тоді

а базисі вектор x має координати , тоді

Оскільки ліві частини останніх двох рівностей однакові, ми можемо прирівняти праві частини:

Якщо помножити обидві частини праворуч на

то отримаємо


З іншого боку

(Знайдіть зворотну матрицю самостійно).
Дві останні рівність дають нам шуканий зв'язок координат вектора x у базисах і .

Відповідь:

Матриця переходу від базису до базису має вигляд
;
координати вектора x у базисах та пов'язані співвідношеннями

або
.

Ми розглянули поняття розмірності та базису векторного простору, навчилися розкладати вектор по базису та виявили зв'язок між різними базисами n-мірного простору векторів через матрицю переходу.

Сторінка 1

Підпростір, його базис та розмірність.

Нехай L- Лінійний простір над полем P і A- підмножина з L. Якщо Aсаме складає лінійний простір над полем Pщодо тих самих операцій, що й L, то Aназивають підпростором простору L.

Відповідно до визначення лінійного простору, щоб Aбуло підпростором треба перевірити здійсненність у Aоперацій:

1) :
;

2)
:
;

і перевірити, що операції в Aпідпорядковані восьми аксіом. Проте останнє буде зайвим (тому що ці аксіоми виконуються в L) тобто. справедлива наступна

Теорема.Нехай L лінійний простір над полем P і
. Безліч A тоді і лише тоді є підпростором L, коли виконуються такі вимоги:

1. :
;

2.
:
.

Твердження.Якщо L – n-мірний лінійний простір та Aйого підпростір, то Aтакож кінцевий лінійний простір і його розмірність не перевищує n.

П ример 1.Чи є підпростором простору векторів-відрізків V2 безліч S всіх векторів площини, кожен з яких лежить на одній з осей координат 0x або 0y?

Рішення: Нехай
,
і
,
. Тоді
. Отже, S не є підпростором .

приклад 2. V 2 векторів-відрізків площини безліч Sвсіх векторів площини, початку та кінці яких лежать на даній прямій lцій площині?

Рішення.

Е слі вектор
помножити на дійсне число k, то отримаємо вектор
, також належить S. Якщо і – два вектори з S, то
(за правилом складання векторів на прямий). Отже, S є підпростором .

Приклад 3.Чи є лінійним підпростором лінійного простору V 2 безліч Aвсіх векторів площини, кінці яких лежать на даній прямій l, (Припустити, що початок будь-якого вектора збігається з початком координат)?

Р ешение.

У разі, коли пряма lне проходить через початок координат безліч Алінійним підпростором простору V 2 не є, т.к.
.

У разі, коли пряма l проходить через початок координат, безліч Ає лінійним підпростором простору V 2 , т.к.
і при множенні будь-якого вектора
на дійсне число α з поля Ротримаємо
. Таким чином, вимоги лінійного простору для множини Авиконані.

Приклад 4.Нехай дана система векторів
з лінійного простору Lнад полем P. Довести, що безліч різноманітних лінійних комбінацій
з коефіцієнтами
з Pє підпростором L(це підпростір Aназивають підпростором, породженим системою векторів
або лінійною оболонкою цієї системи векторів, і позначають так:
або
).

Рішення. Справді, тому що , то для будь-яких елементів x, yAмаємо:
,
, де
,
. Тоді

Так як
, то
тому
.

Перевіримо здійсненність другої умови теореми. Якщо x- будь-який вектор з Aі t– будь-яке число з P, то. Оскільки
і
,
, то
,
тому
. Таким чином, згідно з теореми, безліч A- Простір лінійного простору L.

Для кінцевих лінійних просторів справедливе і зворотне твердження.

Теорема.Будь-який підпростір Алінійного простору Lнад полем є лінійною оболонкою певної системи векторів.

При розв'язанні задачі знаходження базису та розмірності лінійної оболонки використовують наступну теорему.

Теорема.Базис лінійної оболонки
збігається з базисом системи векторів
. Розмірність лінійної оболонки
збігається з рангом системи векторів
.

Приклад 4.Знайти базис та розмірність підпростору
лінійного простору Р 3 [ x] , якщо
,
,
,
.

Рішення. Відомо, що вектори та їх координатні рядки (стовпці) мають однакові властивості (щодо лінійної залежності). Складаємо матрицю A=
з координатних стовпців векторів
у базисі
.

Знайдемо ранг матриці A.

. М 3 =
.
.

Отже, ранг r(A)= 3. Отже, ранг системи векторів
дорівнює 3. Отже, розмірність підпростору S дорівнює 3, яке базис складається з трьох векторів
(т.к. в базовий мінор
входять координати цих векторів)., . Ця система векторів є лінійно незалежною. Справді, нехай.

І
.

Можна переконатися, що система
лінійно залежна за будь-якого вектора xз H. Цим доведено, що
максимальна лінійно незалежна система векторів підпростору H, тобто.
– базис у Hта dim H=n 2 .

сторінка 1

Лінійний простір V називається n-мірнимякщо в ньому існує система з n лінійно незалежних векторів, а будь-яка система з більшої кількості векторів лінійно залежна. Число n називається розмірністю (числом вимірів)лінійного простору V і позначається \operatorname(dim)V. Іншими словами, розмірність простору – це максимальна кількість лінійно незалежних векторів цього простору. Якщо така кількість існує, то простір називається кінцевим. Якщо для будь-якого натурального числа п у просторі V знайдеться система, що складається з n лінійно незалежних векторів, то такий простір називають нескінченномірним (записують: \operatorname(dim)V=\infty). Далі, якщо не обумовлено неприємне, будуть розглядатися кінцеві простори.

Базисом n-мірного лінійного простору називається впорядкована сукупність n лінійно незалежних векторів ( базисних векторів).

Теорема 8.1 про розкладання вектора за базисом. Якщо - базис n-вимірного лінійного простору V , то будь-який вектор \mathbf(v)\in V може бути представлений у вигляді лінійної комбінації базисних векторів:

\mathbf(v)=\mathbf(v)_1\cdot \mathbf(e)_1+\mathbf(v)_2\cdot \mathbf(e)_2+\ldots+\mathbf(v)_n\cdot \mathbf(e)_n

і до того ж єдиним чином, тобто. коефіцієнти \mathbf(v)_1, \mathbf(v)_2,\ldots, \mathbf(v)_nвизначаються однозначно.Іншими словами, будь-який вектор простору може бути розкладений по базису і до того ж єдиним чином.

Справді, розмірність простору V дорівнює n. Система векторів \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_nлінійно незалежна (це базис). Після приєднання до базису будь-якого вектора \mathbf(v) отримуємо лінійно залежну систему \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n, \mathbf(v)(оскільки ця система складається з (n+1) векторів n-мірного простору). За якістю 7 лінійно залежних та лінійно незалежних векторів отримуємо висновок теореми.

Наслідок 1. Якщо \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- базис простору V , то V=\operatorname(Lin) (\mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_n), тобто. Лінійний простір є лінійною оболонкою базисних векторів.

Справді, для доказу рівності V=\operatorname(Lin) (\mathbf(e)_1,\mathbf(e)_2, \ldots, \mathbf(e)_n)двох множин досить показати, що включення V\subset \operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_n)та виконуються одночасно. Справді, з одного боку, будь-яка лінійна комбінація векторів лінійного простору належить самому лінійному простору, тобто. \operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n)\subset V. З іншого боку, будь-який вектор простору за теоремою 8.1 можна як лінійної комбінації базисних векторів, тобто. V\subset \operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n). Звідси випливає рівність розглянутих множин.

Наслідок 2. Якщо \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- лінійно незалежна система векторів лінійного простору V і будь-який вектор \mathbf(v)\in V може бути представлений у вигляді лінійної комбінації (8.4): \mathbf(v)=v_1\mathbf(e)_1+ v_2\mathbf(e)_2+\ldots+v_n\mathbf(e)_n, то простір V має розмірність n а система \mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_nє його базисом.

Насправді, у просторі V є система n лінійно незалежних векторів, а будь-яка система \mathbf(u)_1,\mathbf(u)_2,\ldots,\mathbf(u)_nз більшої кількості векторів (k>n) лінійно залежна, оскільки кожен вектор із цієї системи лінійно виражається через вектори \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n. Значить, \operatorname(dim) V=nі \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- Базис V.

Теорема 8.2 щодо доповнення системи векторів до базису. Будь-яку лінійно незалежну систему k векторів n-мірного лінійного простору (1\leqslant k

Справді, нехай – лінійно незалежна система векторів n-мірного простору V~(1\leqslant k . Розглянемо лінійну оболонку цих векторів: L_k=\operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots, \mathbf(e)_k). Будь-який вектор \mathbf(v)\in L_kутворює із векторами \mathbf(e)_1,\mathbf(e)_2,\ldots, \mathbf(e)_kлінійно залежну систему \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_k,\mathbf(v), Оскільки вектор \mathbf(v) лінійно виражається через інші. Оскільки в n-мірному просторі існує n лінійно незалежних векторів, то L_k\ne V і існує вектор \mathbf(e)_(k+1)\in Vщо не належить L_k . Доповнюючи цим вектором лінійно незалежну систему \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_k, отримуємо систему векторів \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_k,\mathbf(e)_(k+1), яка також є лінійно незалежною. Справді, якби вона була лінійно залежною, то з пункту 1 зауважень 8.3 випливало, що \mathbf(e)_(k+1)\in \operatorname(Lin)(\mathbf(e)_1, \mathbf(e)_2, \ldots,\mathbf(e)_k)=L_k, а це суперечить умові \mathbf(e)_(k+1)\notin L_k. Отже, система векторів \mathbf(e)_1,\mathbf(e)_2,\ldots, \mathbf(e)_k, \mathbf(e)_(k+1)лінійно незалежна. Отже, початкову систему векторів вдалося доповнити одним вектором без порушення лінійної незалежності. Продовжуємо аналогічно. Розглянемо лінійну оболонку цих векторів: L_(k+1)=\operatorname(Lin) (\mathbf(e)_1, \mathbf(e)_2,\ldots, \mathbf(e)_k, \mathbf(e)_(k+1)). Якщо L_(k+1)=V , то \mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_k, \mathbf(e)_(k+1)- базис та теорема доведена. Якщо L_(k+1)\ne V , то доповнюємо систему \mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_k,\mathbf(e)_(k+1)вектором \mathbf(e)_(k+2)\notin L_(k+1)і т.д. Процес доповнення обов'язково закінчиться, оскільки простір V є кінцевим. В результаті отримаємо рівність V=L_n=\operatorname(Lin) (\mathbf(e)_1,\ldots,\mathbf(e)_k,\ldots,\mathbf(e)_n), з якого випливає, що \mathbf(e)_1,\ldots,\mathbf(e)_k,\ldots,\mathbf(e)_n- Базис простору V. Теорему доведено.

Зауваження 8.4

1. Базис лінійного простору визначається неоднозначно. Наприклад, якщо \mathbf(e)_1,\mathbf(e)_2, \ldots, \mathbf(e)_n- базис простору V , то система векторів \lambda \mathbf(e)_1,\lambda \mathbf(e)_2,\ldots,\lambda \mathbf(e)_nза будь-якого \lambda\ne0 також є базисом V . Кількість базисних векторів у різних базисах однієї й тієї ж конечномерного простору, очевидно, те саме, оскільки це кількість дорівнює розмірності простору.

2. У деяких просторах, які часто зустрічаються в додатках, один з можливих базисів, найбільш зручний з практичної точки зору, називають стандартним.

3. Теорема 8.1 дозволяє говорити, що базис - це повна система елементів лінійного простору, тому, що будь-який вектор простору лінійно виражається через базисні вектори.

4. Якщо безліч \mathbb(L) є лінійною оболонкою \operatorname(Lin)(\mathbf(v)_1,\mathbf(v)_2,\ldots,\mathbf(v)_k), то вектори \mathbf(v)_1,\mathbf(v)_2,\ldots,\mathbf(v)_kназивають утворюючими множини \mathbb(L) . Наслідок 1 теореми 8.1 через рівність V=\operatorname(Lin) (\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n)дозволяє казати, що базис - це мінімальна система утворюючихлінійного простору V , тому що не можна зменшити кількість утворюючих (видалити хоча б один вектор з набору \mathbf(e)_1, \mathbf(e)_2,\ldots,\mathbf(e)_n) без порушення рівності V=\operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n).

5. Теорема 8.2 дозволяє говорити, що базис – це максимальна лінійно незалежна система векторівлінійного простору, оскільки базис - це лінійно незалежна система векторів, і його не можна доповнити будь-яким вектором без втрати лінійної незалежності.

6. Наслідок 2 теореми 8.1 зручно застосовувати для знаходження базису та розмірності лінійного простору. У деяких підручниках воно береться за визначення базису, а саме: лінійно незалежна система \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_nвекторів лінійного простору називається базисом, якщо будь-який вектор простору лінійно виражається через вектори \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n. Кількість базисних векторів визначає розмірність простору. Вочевидь, що це визначення еквівалентні наведеним вище.

Приклади базисів лінійних просторів

Вкажемо розмірність і базис для прикладів лінійних просторів, розглянутих вище.

1. Нульовий лінійний простір \(\mathbf(o)\) не містить лінійно незалежних векторів. Тому розмірність цього простору вважають рівною нулю: \dim\(\mathbf(o)\)=0. Цей простір немає базису.

2. Простори V_1,\,V_2,\,V_3 мають розмірності 1, 2, 3 відповідно. Дійсно, будь-який ненульовий вектор простору V_1 утворює лінійно незалежну систему (див. пункт 1. зауважень 8.2), а будь-які два ненульові вектори простору V_1 колінеарні, тобто. лінійно залежні (див. приклад 8.1). Отже, \dim(V_1)=1 , а базисом простору V_1 є будь-який вектор. Аналогічно доводиться, що \dim(V_2)=2 та \dim(V_3)=3 . Базисом простору V_2 служать будь-які два неколлінеарні вектори, взяті в певному порядку (один з них вважається першим базисним вектором, інший - другим). Базисом простору V_3 є будь-які три некомпланарні (що не лежать в одній або паралельних площинах) вектора, взяті в певному порядку. Стандартним базисом V_1 є одиничний вектор \ vec (i) на прямий. Стандартним базисом у V_2 вважається базис \vec(i),\,\vec(j), що складається із двох взаємно перпендикулярних одиничних векторів площини. Стандартним базисом у просторі V_3 вважається базис \vec(i),\,\vec(j),\,\vec(k), Складений з трьох одиничних попарно перпендикулярних векторів, що утворюють праву трійку

3. Простір \mathbb(R)^n містить не більше, ніж n лінійно незалежних векторів. Справді, візьмемо k стовпців \mathbb(R)^n і складемо з них матрицю розмірів n\times k . Якщо k>n то стовпці лінійно залежні за теоремою 3.4 про ранг матриці. Отже, \dim(\mathbb(R)^n)\leqslant n. У просторі \mathbb(R)^n не важко знайти лінійно незалежних стовпців. Наприклад, стовпці одиничної матриці

\mathbf(e)_1=\begin(pmatrix)1\\0\\\vdots\\0\end(pmatrix)\!,\quad \mathbf(e)_2= \begin(pmatrix)0\\1\ \\vdots\\0\end(pmatrix)\!,\quad \ldots,\quad \mathbf(e)_n= \begin(pmatrix) 0\\0\\vdots\\1 \end(pmatrix)\ !.

лінійно незалежні. Отже, \dim(\mathbb(R)^n)=n. Простір \mathbb(R)^n називається n-мірним речовим арифметичним простором. Зазначений набір векторів вважається стандартним базисом простору \mathbb(R)^n. Аналогічно доводиться, що \dim(\mathbb(C)^n)=nтому простір \mathbb(C)^n називають n-мірним комплексним арифметичним простором.

4. Нагадаємо, що будь-яке рішення однорідної системи Ax=o можна подати у вигляді x=C_1\varphi_1+C_2\varphi_2+\ldots+C_(n-r)\varphi_(n-r), де r=\operatorname(rg)A, a \varphi_1,\varphi_2,\ldots,\varphi_(n-r)– фундаментальна система рішень. Отже, \(Ax=o\)=\operatorname(Lin) (\varphi_1,\varphi_2,\ldots,\varphi_(n-r)), тобто. базисом простору \(Ax=0\) рішень однорідної системи служить її фундаментальна система рішень, а розмірність простору \dim\(Ax=o\)=n-r де n - кількість невідомих, а r - ранг матриці системи.

5. У просторі M_(2\times3) матриць розмірів 2\times3 можна вибрати 6 матриць:

\begin(gathered)\mathbf(e)_1= \begin(pmatrix)1&0&0\\0&0&0\end(pmatrix)\!,\quad \mathbf(e)_2= \begin(pmatrix)0&1&0\\0&0&0\end( pmatrix)\!,\quad \mathbf(e)_3= \begin(pmatrix) 0&0&1\\0&0&0\end(pmatrix)\!,\hfill\\ \mathbf(e)_4= \begin(pmatrix) 0&0&0\\ 1&0&0 \end(pmatrix)\!,\quad \mathbf(e)_5= \begin(pmatrix)0&0&0\\0&1&0\end(pmatrix)\!,\quad \mathbf(e)_6= \begin(pmatrix)0&0&0 \\0&0&1\end(pmatrix)\!,\hfill \end(gathered)

які лінійно незалежні. Справді, їхня лінійна комбінація

\alpha_1\cdot \mathbf(e)_1+\alpha_2\cdot \mathbf(e)_2+\alpha_3\cdot \mathbf(e)_3+ \alpha_4\cdot \mathbf(e)_4+\alpha_5\cdot \math \alpha_6\cdot \mathbf(e)_6= \begin(pmatrix)\alpha_1&\alpha_2&\alpha_3\\ \alpha_4&\alpha_5&\alpha_6\end(pmatrix)

дорівнює нульовій матриці лише у тривіальному випадку \alpha_1=\alpha_2= \ldots= \alpha_6=0. Прочитавши рівність (8.5) справа наліво, укладаємо, що кожна матриця з M_(2\times3) лінійним чином виражається через вибрані 6 матриць, тобто. M_(2\times)= \operatorname(Lin) (\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_6). Отже, \dim(M_(2\times3))=2\cdot3=6, а матриці \mathbf(e)_1, \mathbf(e)_2,\ldots,\mathbf(e)_6є базисом (стандартним) цього простору. Аналогічно доводиться, що \dim(M_(m\times n))=m\cdot n.

6. Для будь-якого натурального n у просторі P(\mathbb(C)) багаточленів з комплексними коефіцієнтами можна знайти лінійно незалежних елементів. Наприклад, багаточлени \mathbf(e)_1=1, \mathbf(e)_2=z, \mathbf(e)_3=z^2,\,\ldots, \mathbf(e)_n=z^(n-1)лінійно незалежні, оскільки їхня лінійна комбінація

a_1\cdot \mathbf(e)_1+a_2\cdot \mathbf(e)_2+\ldots+a_n\cdot \mathbf(e)_n= a_1+a_2z+\ldots+a_nz^(n-1)

дорівнює нульовому багаточлену (o(z)\equiv0) лише у тривіальному випадку a_1=a_2=\ldots=a_n=0. Оскільки ця система багаточленів лінійно незалежна за будь-якого натурального л, простір P(\mathbb(C)) нескінченномірний. Аналогічно робимо висновок про нескінченну розмірність простору P(\mathbb(R)) багаточленів з дійсними коефіцієнтами. Простір P_n(\mathbb(R)) багаточленів ступеня не вище, ніж n кінцевий. Дійсно, вектори \mathbf(e)_1=1, \mathbf(e)_2=x, \mathbf(e)_3=x^2,\,\ldots, \mathbf(e)_(n+1)=x^nутворюють базис (стандартний) цього простору, так як вони лінійно незалежні і будь-який многочлен з P_n(\mathbb(R)) можна представити у вигляді лінійної комбінації цих векторів:

a_nx^n+\ldots+a_1x+a_0=a_0\cdot \mathbf(e)_1+a_1 \mathbf(e)_2+\ldots+a_n\cdot \mathbf(e)_(n+1). Отже, \dim(P_n(\mathbb(R)))=n+1.

7. Простір C(\mathbb(R)) безперервних функцій є нескінченно мірним. Справді, для будь-якого натурального n багаточлени 1,x,x^2,\ldots, x^(n-1), Які розглядаються як безперервні функції, утворюють лінійно незалежні системи (див. попередній приклад).

В просторі T_(\omega)(\mathbb(R))тригонометричних двочленів (частоти \omega\ne0 ) з дійсними коефіцієнтами базис утворюють одночлени \mathbf(e)_1(t)=\sin\omega t,~\mathbf(e)_2(t)=\cos\omega t. Вони лінійно незалежні, оскільки тотожна рівність a\sin\omega t+b\cos\omega t\equiv0можливо лише у тривіальному випадку (a=b=0) . Будь-яка функція виду f(t)=a\sin\omega t+b\cos\omega tлінійно виражається через базисні: f(t)=a\,\mathbf(e)_1(t)+b\,\mathbf(e)_2(t).

8. Простір \mathbb(R)^X дійсних функцій, визначених на множині X, залежно від області визначення X може бути кінцевим або нескінченним. Якщо X - кінцева множина, то простір \mathbb(R)^X кінцевий (наприклад, X=\(1,2,\ldots,n\)). Якщо X - безліч, то простір \mathbb(R)^X нескінченномірний (наприклад, простір \mathbb(R)^N послідовностей).

9. У просторі \mathbb(R)^(+) будь-яке позитивне число \mathbf(e)_1 , не рівне одиниці, може бути базисом. Візьмемо, наприклад, число \mathbf(e)_1=2. Будь-яке позитивне число r можна сказати через \mathbf(e)_1 , тобто. уявити у вигляді \alpha\cdot \mathbf(e)_1\colon r=2^(\log_2r)=\log_2r\ast2=\alpha_1\ast \mathbf(e)_1, де \alpha_1=\log_2r. Отже, розмірність цього простору дорівнює 1, число \mathbf(e)_1=2 є базисом.

10. Нехай \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- Базис речового лінійного простору V. Визначимо на V лінійні скалярні функції, поклавши:

\mathcal(E)_i(\mathbf(e)_j)=\begin(cases)1,&i=j,\\ 0,&i\ne j.\end(cases)

При цьому, в силу лінійності функції \mathcal(E)_i для довільного вектора отримуємо \mathcal(E)(\mathbf(v))=\sum_(j=1)^(n)v_j \mathcal(E)(\mathbf(e)_j)=v_i.

Отже, визначено n елементів (ковекторів) \mathcal(E)_1, \mathcal(E)_2, \ldots, \mathcal(E)_nсполученого простору V^(\ast) . Доведемо, що \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_n- Базис V^(\ast).

По-перше, покажемо, що система \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_nлінійно незалежна. Справді, візьмемо лінійну комбінацію цих ковекторів (\alpha_1 \mathcal(E)_1+\ldots+\alpha_n\mathcal(E)_n)(\mathbf(v))=та прирівняємо її нульовій функції

\mathbf(o)(\mathbf(v))~~ (\mathbf(o)(\mathbf(v))=0~ \forall \mathbf(v)\in V)\colon~ \alpha_1\mathcal(E )_1(\mathbf(v))+\ldots+\alpha_n\mathcal(E)_n(\mathbf(v))= \mathbf(o)(\mathbf(v))=0~~\forall \mathbf(v )\in V.

Підставляючи в цю рівність \mathbf(v)=\mathbf(e)_i,~ i=1,\ldots,n, отримуємо \alpha_1=\alpha_2\cdot= \alpha_n=0. Отже, система елементів \mathcal(E)_1,\mathcal(E)_2,\ldots,\mathcal(E)_nпростору V^(\ast) лінійно незалежна, тому що рівність \alpha_1\mathcal(E)_1+\ldots+ \alpha_n\mathcal(E)_n =\mathbf(o)можливо лише у тривіальному випадку.

По-друге, доведемо, що будь-яку лінійну функцію f\in V^(\ast) можна у вигляді лінійної комбінації ковекторів \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_n. Дійсно, для будь-якого вектору \mathbf(v)=v_1 \mathbf(e)_1+v_2 \mathbf(e)_2+\ldots+v_n \mathbf(e)_nчерез лінійність функції f отримуємо:

\begin(aligned)f(\mathbf(v))&= f(v_1 \mathbf(e)_1+\ldots+v_n \mathbf(e)_n)= v_1 f(\mathbf(e)_1)+\ldots+ v_n f(\mathbf(e)_n)= f(\mathbf(e)_1)\mathcal(E)_1(\mathbf(v))+ \ldots+ f(\mathbf(e)_n)\mathcal(E) _n(\mathbf(v))=\\ &=(f(\mathbf(e)_1)\mathcal(E)_1+\ldots+ f(\mathbf(e)_n)\mathcal(E)_n)(\mathbf (v))= (\beta_1\mathcal(E)_1+ \ldots+\beta_n\mathcal(E)_n) (\mathbf(v)),\end(aligned)

тобто. функція f представлена ​​у вигляді лінійної комбінації f=\beta_1 \mathcal(E)_1+\ldots+\beta_n\mathcal(E)_nфункцій \mathcal(E)_1,\mathcal(E)_2,\ldots, \mathcal(E)_n(числа \beta_i=f(\mathbf(e)_i)- Коефіцієнти лінійної комбінації). Отже, система ковекторів \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_nє базисом сполученого простору V^(\ast) і \dim(V^(\ast))=\dim(V)(Для кінцевого простору V ).

Якщо помітили помилку, друкарську помилку або є пропозиції, напишіть у коментарях.

Системи лінійних однорідних рівнянь

Постановка задачі. Знайти якийсь базис та визначити розмірність лінійного простору рішень системи

План розв'язання.

1. Записуємо матрицю системи:

і з допомогою елементарних перетворень перетворимо матрицю до трикутному виду, тобто. до такого виду, коли всі елементи, що знаходяться нижче за головну діагональ дорівнюють нулю. Ранг матриці системи дорівнює числу лінійно незалежних рядків, тобто, у нашому випадку, числу рядків, в яких залишилися ненульові елементи:

Розмірність простору рішень дорівнює. Якщо , то однорідна система має єдине нульове рішення, якщо , то система має безліч рішень.

2. Вибираємо базисних та вільних змінних. Вільні змінні позначаємо. Потім базисні змінні виражаємо через вільні, отримавши таким чином загальне рішення однорідної системи лінійних рівнянь.

3. Записуємо базис простору рішень системи вважаючи послідовно одну з вільних змінних рівної одиниці, інші ж нулю. Розмірність лінійного простору рішень системи дорівнює кількості векторів базису.

Примітка. До елементарних перетворень матриці відносять:

1. множення (розподіл) рядка на множник, відмінний від нуля;

2. додавання до будь-якого рядка іншого рядка, помноженого на будь-яке число;

3. перестановка рядків подекуди;

4. перетворення 1–3 для стовпців (у разі розв'язання систем лінійних рівнянь елементарні перетворення стовпців не використовуються).

Завдання 3.Знайти якийсь базис і визначити розмірність лінійного простору рішень системи.

Виписуємо матрицю системи та за допомогою елементарних перетворень наводимо її до трикутного вигляду:

Вважаємо, тоді