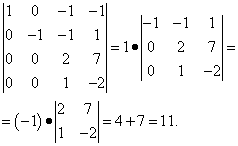Подальші властивості пов'язані з поняттями мінору та алгебраїчного доповнення
Міноромелемента називається визначник, складений із елементів, що залишилися після викреслення стоки та стовпця, на перетині яких знаходиться цей елемент. Мінор елемента визначника порядку має порядок. Будемо його позначати через .
приклад 1.Нехай 
тоді 
.
Цей мінор виходить з A шляхом викреслення другого рядка та третього стовпця.
Алгебраїчним доповненнямелемента називається відповідний мінор, помножений на , тобто 
, де номер рядка і -стовпця, на перетині яких знаходиться даний елемент.
VІІІ.(Розкладання визначника за елементами деякого рядка). Визначник дорівнює сумі творів елементів деякого рядка на відповідні їм додатки алгебри.
приклад 2.Нехай 
тоді
Приклад 3.Знайдемо визначник матриці , розклавши його за елементами першого рядка
Формально ця теорема та інші властивості визначників застосовні поки що лише для визначників матриць не вище третього порядку, оскільки інші визначники ми не розглядали. Наступне визначення дозволить поширити ці властивості на визначники будь-якого порядку.
Визначником матриці порядкуназивається число, обчислене за допомогою послідовного застосування теореми про розкладання та інші властивості визначників.
Можна перевірити, що результат обчислень не залежить від того, в якій послідовності та для яких рядків та стовпців застосовуються вищезазначені властивості. Визначник за допомогою цього визначення є однозначним.
Хоча це визначення не містить явної формули для знаходження визначника, воно дозволяє знаходити його шляхом зведення до визначників матриць меншого порядку. Такі визначення називають рекурентними.
Приклад 4.Обчислити визначник: 
Хоча теорему про розкладання можна застосовувати до будь-якого рядка або стовпця даної матриці, менше обчислень вийде при розкладанні по стовпцю, що містить якнайбільше нулів.
Оскільки матриця не має нульових елементів, то отримаємо їх за допомогою властивості VII. Помножимо перший рядок послідовно на числа 
і додамо її до рядків і отримаємо:
Розкладемо визначник по першому стовпцю і отримаємо:
оскільки визначник містить два пропорційні стовпці.
Деякі види матриць та їх визначники
Квадратна матриця, у якої нижче або вище за головну діагональ стоять нульові елементи ()називається трикутної.
Їх схематична будова відповідно має вигляд: 
або
.
У ході вирішення завдань з вищої математики часто виникає необхідність обчислити визначник матриці. Визначник матриці фігурує у лінійній алгебрі, аналітичній геометрії, математичному аналізі та інших розділах вищої математики. Таким чином, без навички вирішення визначників просто не обійтись. Також для самоперевірки Ви можете безкоштовно скачати калькулятор визначників, він сам по собі не навчить вирішувати визначники, але дуже зручний, оскільки завжди вигідно знати правильну відповідь!
Я не даватиму строгого математичного визначення визначника, і, взагалі, намагатимуся мінімізувати математичну термінологію, більшості читачів легше від цього не стане. Завдання цієї статті – навчити Вас вирішувати визначники другого, третього та четвертого порядку. Весь матеріал викладений у простій та доступній формі, і навіть повний (порожній) чайник у вищій математиці після уважного вивчення матеріалу зможе правильно вирішувати визначники.
Насправді найчастіше можна зустріти визначник другого порядку, наприклад: , і визначник третього порядку, наприклад: 
.
Визначник четвертого порядку 
теж не антикваріат, і до нього ми підійдемо наприкінці уроку.
Сподіваюся, всім зрозуміло таке:Числа всередині визначника живуть самі по собі, і ні про яке віднімання не йдеться! Міняти місцями числа не можна!
(Як зокрема, можна здійснювати парні перестановки рядків або стовпців визначника зі зміною його знака, але часто в цьому немає жодної необхідності – див. наступний урок Властивості визначника та зниження його порядку)
Таким чином, якщо дано якийсь визначник, то нічого всередині нього не чіпаємо!
Позначення: Якщо дана матриця 
, її визначник позначають . Також дуже часто визначник позначають латинською літерою або грецькою.
1)Що означає вирішити (знайти, розкрити) визначник?Обчислити визначник – це означає ЗНАЙТИ ЧИСЛО. Знаки питання у вищерозглянутих прикладах – це прості числа.
2) Тепер залишилося розібратися в тому, Як знайти це число?Для цього потрібно застосувати певні правила, формули та алгоритми, про що зараз і йтиметься.
Почнемо з визначника "два" на "два":
Це потрібно запам'ятати, принаймні на час вивчення вищої математики у ВНЗ.
Відразу розглянемо приклад:
Готово. Найголовніше, НЕ ЗАПУТАТИСЯ У ЗНАКАХ.
Визначник матриці "три на три"можна розкрити 8 способами, 2 їх прості і 6 - нормальні.
Почнемо з двох простих способів
Аналогічно визначнику "два на два", визначник "три на три" можна розкрити за допомогою формули:
Формула довга і припуститися помилки по неуважності простіше простого. Як уникнути прикрих промахів? І тому придуманий другий спосіб обчислення визначника, який збігається з першим. Називається він способом Саррюса або способом «паралельних смужок».
Суть полягає в тому, що праворуч від визначника приписують перший і другий стовпець і акуратно олівцем проводять лінії:
Численні, що знаходяться на «червоних» діагоналях, входять у формулу зі знаком «плюс».
Численні, що знаходяться на «синіх» діагоналях, входять у формулу зі знаком мінус:
Приклад:
Порівняйте два рішення. Неважко помітити, що це ОДНЕ І ТЕ, просто в другому випадку трохи переставлені множники формули, і, найголовніше, ймовірність припуститися помилки значно менше.
Тепер розглянемо шість нормальних способів обчислення визначника
Чому нормальні? Тому що у переважній більшості випадків визначники потрібно розкривати саме так.
Як Ви помітили, у визначника «три на три» три стовпці та три рядки.
Вирішити визначник можна, розкривши його за будь-яким рядком або за будь-яким стовпцем.
Таким чином, виходить 6 способів, при цьому завжди використовується однотипнийалгоритм.
Визначник матриці дорівнює сумі творів елементів рядка (стовпця) на відповідні додатки алгебри. Страшно? Все набагато простіше будемо використовувати ненауковий, але зрозумілий підхід, доступний навіть для людини, далекої від математики.
У наступному прикладі розкриватимемо визначник по першому рядку.
І тому нам знадобиться матриця символів: . Легко помітити, що знаки розташовані у шаховому порядку.
Увага! Матриця знаків – це мій власний винахід. Дане поняття не наукове, його не потрібно використовувати в чистовому оформленні завдань, воно допомагає Вам зрозуміти алгоритм обчислення визначника.
Спершу я наведу повне рішення. Знову беремо наш піддослідний визначник і проводимо обчислення:
І головне питання: ЯК з визначника «три на три» отримати ось це:
?
Отже, визначник "три на три" зводиться до вирішення трьох маленьких визначників, або як їх ще називають, МІНОРІВ. Термін рекомендую запам'ятати, тим більше він запам'ятовується: мінор - маленький.
Якщо вибраний спосіб розкладання визначника по першому рядку, очевидно, що все обертається навколо неї:
Елементи зазвичай розглядають ліворуч (або зверху вниз, якщо був би обраний стовпець)
Поїхали, спочатку розбираємось з першим елементом рядка, тобто з одиницею:
1) З матриці знаків виписуємо відповідний знак:
2) Потім записуємо сам елемент:
3) ДУМКОВО викреслюємо рядок і стовпець, у якому стоїть перший елемент:
Чотири числа, що залишилися, і утворюють визначник «два на два», який називається МІНОРОМданого елемента (одиниці).
Переходимо до другого елемента рядка.
4) З матриці знаків виписуємо відповідний знак:
5) Потім записуємо другий елемент:
6) ДУМКОВО викреслюємо рядок і стовпець, у якому стоїть другий елемент:
Ну і третій елемент першого рядка. Жодної оригінальності:
7) З матриці знаків виписуємо відповідний знак:
8) Записуємо третій елемент:
9) ДУМКОВО викреслюємо рядок і стовпець, у якому стоїть третій елемент:
Чотири числа, що залишилися, записуємо в маленький визначник.
Інші дії не становлять труднощів, оскільки визначники «два на два» ми вважати вже вміємо. НЕ ПЛУТАЄМОСЯ У ЗНАКАХ!
Аналогічно визначник можна розкласти за будь-яким рядком або за будь-яким стовпцем.Звичайно, у всіх шести випадках відповідь виходить однаковою.
Визначник «чотири на чотири» можна обчислити, використовуючи той самий алгоритм.
При цьому матриця знаків у нас збільшиться:
У наступному прикладі я розкрив визначник по четвертому стовпцю:
А як це вийшло, спробуйте розібратися самостійно. Додаткова інформація буде пізніше. Якщо хтось захоче вирішувати визначник до кінця, правильна відповідь: 18. Для тренування краще розкрити визначник по якомусь іншому стовпцю або іншому рядку.
Потренуватися, розкрити, провести розрахунки – це дуже добре та корисно. Але скільки часу ви витратите на великий визначник? Чи не можна якось швидше і надійніше? Пропоную ознайомитись з ефективними методами обчислення визначників на другому уроці – Властивості визначника. Зниження порядку визначника.
БУДЬТЕ УВАЖНІ!
Постановка задачі
Завдання має на увазі знайомство користувача з основними поняттями чисельних методів, такими як визначник та зворотна матриця, та різними способами їх обчислень. У даному теоретичному звіті простою та доступною мовою спочатку вводяться основні поняття та визначення, на підставі яких проводиться подальше дослідження. Користувач може не мати спеціальних знань у галузі чисельних методів та лінійної алгебри, але легко зможе скористатися результатами даної роботи. Для наочності наведено програму обчислення визначника матриці декількома методами, написану мовою програмування C++. Програма використається як лабораторний стенд для створення ілюстрацій до звіту. А також проводиться дослідження методів для вирішення систем лінійних рівнянь алгебри . Доводиться марність обчислення зворотної матриці, у роботі наводиться найбільш оптимальні способи розв'язання рівнянь не обчислюючи її. Розповідається чому існує така кількість різних методів обчислення визначників та зворотних матриць та розбираються їхні недоліки. Також розглядаються похибки при обчисленні визначника та оцінюється досягнута точність. Крім російських термінів у роботі застосовуються та його англійські еквіваленти розуміння, під якими назвами шукати чисельні процедури у бібліотеках і що означають їх параметри.
Основні визначення та найпростіші властивості
Визначник
Введемо визначення визначника квадратної матриці будь-якого порядку. Це визначення буде рекурентним, тобто встановити, що таке визначник матриці порядку , потрібно знати, що таке визначник матриці порядку . Зазначимо також, що визначник існує лише у квадратних матриць.
Визначник квадратної матриці будемо позначати або det.
Визначення 1. Визначникомквадратної матриці 
другого порядку називається число 
.
Визначником 
квадратної матриці порядку , називається число 
де - визначник матриці порядку, отриманої з матриці викреслюванням першого рядка та стовпця з номером.
Для наочності запишемо, як можна обчислити визначник матриці четвертого порядку:
Зауваження.Реальне обчислення визначників для матриць вище за третій порядок на основі визначення використовується у виняткових випадках. Як правило, обчислення ведеться за іншими алгоритмами, які будуть розглянуті пізніше та які вимагають менше обчислювальної роботи.
Зауваження.У визначенні 1 було б точніше сказати, що визначник є функція, визначена на множині квадратних матриць порядку і приймає значення у множині чисел.
Зауваження.У літературі замість терміна "визначник" використовується також термін "детермінант", що має той самий сенс. Від слова "детермінант" і з'явилося позначення det.
Розглянемо деякі властивості визначників, які сформулюємо як тверджень.
Твердження 1.При транспонуванні матриці визначник не змінюється, тобто .
Твердження 2.Визначник добутку квадратних матриць дорівнює добутку визначників співмножників, тобто .
Твердження 3.Якщо в матриці поміняти місцями два рядки, її визначник змінить знак.
Твердження 4.Якщо матриця має два однакові рядки, то її визначник дорівнює нулю.
Надалі нам потрібно складати рядки і множити рядок на число. Ці дії над рядками (стовпцями) ми виконуватимемо так само, як дії над матрицями-рядками (матрицями-стовпцями), тобто поелементно. Результатом буде служити рядок (стовпець), як правило, що не збігається з рядками вихідної матриці. За наявності операцій складання рядків (стовпців) та множення їх на число ми можемо говорити і про лінійні комбінації рядків (стовпців), тобто суми з числовими коефіцієнтами.
Твердження 5.Якщо рядок матриці помножити на число , її визначник помножиться на це число.
Твердження 6.Якщо матриця містить нульовий рядок, її визначник дорівнює нулю.
Твердження 7.Якщо один із рядків матриці дорівнює іншому, помноженому на число (рядки пропорційні), то визначник матриці дорівнює нулю.
Твердження 8.Нехай у матриці перший рядок має вигляд . Тоді, де матриця виходить з матриці заміною i-го рядка на рядок, а матриця - заміною i-го рядка на рядок.
Твердження 9.Якщо до одного з рядків матриці додати інший, помножений на число, то визначник матриці не зміниться.
Твердження 10.Якщо один із рядків матриці є лінійною комбінацією інших її рядків, то визначник матриці дорівнює нулю.
Визначення 2. Алгебраїчним доповненнямдо елемента матриці називається число, що дорівнює , де - визначник матриці, отриманої з матриці викреслюванням i-го рядка і j-ого стовпця. Алгебраїчне доповнення до елемента матриці позначається.
приклад.Нехай 
. Тоді 
Зауваження.Використовуючи додатки алгебри, визначення 1 визначника можна записати так: 
Твердження 11. Розкладання визначника по довільному рядку.
Для визначника матриці справедлива формула 
приклад.Обчисліть 
.
Рішення.Скористаємося розкладанням по третьому рядку, так вигідніше, оскільки у третьому рядку два числа з трьох – нулі. Отримаємо
Твердження 12.Для квадратної матриці порядку при виконано співвідношення 
.
Твердження 13.Всі властивості визначника, сформульовані для рядків (затвердження 1 - 11), справедливі і для стовпців, зокрема, справедливе розкладання визначника по j-му стовпцю 
і рівність 
при .
Твердження 14.Визначник трикутної матриці дорівнює добутку елементів головної діагоналі.
Наслідок.Визначник одиничної матриці дорівнює одиниці, .
Висновок.Наведені вище властивості дозволяють знаходити визначники матриць досить високих порядків при порівняно невеликому обсязі обчислень. Алгоритм обчислень наступний.
Алгоритм створення нулів у стовпці.Нехай потрібно обчислити визначник порядку. Якщо , то поміняємо місцями перший рядок і будь-який інший, в якому перший елемент не нуль. В результаті визначник буде дорівнювати визначнику нової матриці з протилежним знаком. Якщо перший елемент кожного рядка дорівнює нулю, то матриця має нульовий стовпець і за твердженнями 1, 13 її визначник дорівнює нулю.
Отже, вважаємо, що вже у вихідній матриці . Перший рядок залишаємо без змін. Додамо до другого рядка перший рядок, помножений на число . Тоді перший елемент другого рядка дорівнюватиме 
.
Інші елементи нового другого рядка позначимо , . Визначник нової матриці за твердженням 9 дорівнює. Перший рядок помножимо на число і додамо до третього. Перший елемент нового третього рядка дорівнюватиме 
Інші елементи нового третього рядка позначимо , . Визначник нової матриці за твердженням 9 дорівнює.
Процес отримання нулів замість перших елементів рядків продовжимо далі. Нарешті, перший рядок помножимо на число і додамо до останнього рядка. В результаті виходить матриця, позначимо її, яка має вигляд 
причому. Для обчислення визначника матриці використовуємо розкладання першого стовпця
Оскільки , то 
У правій частині стоїть визначник матриці порядку. До нього застосовний той самий алгоритм, і обчислення визначника матриці зведеться до обчислення визначника матриці . Процес повторюємо доти, доки дійдемо до визначника другого порядку, який обчислюється за визначенням.
Якщо матриця не має якихось специфічних властивостей, то помітно зменшити обсяг обчислень порівняно із запропонованим алгоритмом не вдається. Ще один добрий бік цього алгоритму - у ньому легко скласти програму для комп'ютера обчислення визначників матриць великих порядків. У стандартних програмах обчислення визначників використовується цей алгоритм з не важливими змінами, пов'язаними з мінімізацією впливу помилок округлення та похибок вхідних даних при обчисленнях комп'ютера.
приклад.Обчисліть визначник матриці 
.
Рішення.Перший рядок залишаємо без зміни. До другого рядка додаємо перший, помножений на число:
Визначник не змінюється. До третього рядка додаємо перший, помножений на число:
Визначник не змінюється. До четвертого рядка додаємо перший, помножений на число:
Визначник не змінюється. В результаті отримуємо 
За тим самим алгоритмом вважаємо визначник матриці порядку 3, що стоїть праворуч. Перший рядок залишаємо без змін, до другого рядка додаємо перший, помножений на число 
:
До третього рядка додаємо перший, помножений на число 
:
В результаті отримуємо
Відповідь. .
Зауваження.Хоча при обчислення використовувалися дроби, результат виявився цілим числом. Справді, використовуючи властивості визначників і те, що вихідні числа - цілі, операцій із дробами можна було б уникнути. Але в інженерній практиці числа дуже рідко бувають цілими. Тому, як правило, елементи визначника будуть десятковими дробами та застосовувати якісь хитрощі для спрощення обчислень недоцільно.
зворотна матриця
Визначення 3.Матриця називається зворотною матрицеюдля квадратної матриці, якщо.
З визначення випливає, що зворотна матриця буде квадратною матрицею того ж порядку, що й матриця (інакше один із творів або було б не визначено).
Зворотна матриця для матриці позначається. Отже, якщо існує, то .
З визначення зворотної матриці слід, що матриця є зворотною для матриці , тобто . Про матриці можна говорити, що вони зворотні один одному або взаємно зворотні.
Якщо визначник матриці дорівнює нулю, зворотна до неї не існує.
Оскільки знаходження зворотної матриці важливо, дорівнює визначник мариці нулю чи ні, то введемо такі визначення.
Визначення 4.Квадратну матрицю назвемо виродженоюабо особливою матрицею, якщо і невиродженоюабо неособливою матрицеюякщо .
Твердження.Якщо зворотна матриця існує, вона єдина.
Твердження.Якщо квадратна матриця є невироджена, то зворотна для неї існує і 
(1) де - Додатки алгебри до елементів .
Теорема.Зворотна матриця для квадратної матриці існує тоді й тільки тоді, коли матриця - невироджена, зворотна матриця єдина і справедлива формула (1).
Зауваження.Слід звернути особливу увагу на місця, що займаються додатками алгебри у формулі зворотної матриці: перший індекс показує номер стовпця, а другий – номер рядки, які потрібно записати обчислене алгебраїчне доповнення.
приклад. 
.
Рішення.Знаходимо визначник
Оскільки , то матриця - невироджена, і обернена нею існує. Знаходимо додатки алгебри:
Складаємо зворотну матрицю, розміщуючи знайдені додатки алгебри так, щоб перший індекс відповідав стовпцю, а другий - рядку: 
(2)
Отримана матриця (2) і є відповіддю до завдання.
Зауваження.У попередньому прикладі було б точніше відповідь записати так:
(3)
Проте запис (2) більш компактний і з ним зручніше проводити подальші обчислення, якщо такі будуть потрібні. Тому запис відповіді у вигляді (2) краще, якщо елементи матриць - цілі числа. І навпаки, якщо елементи матриці – десяткові дроби, то зворотну матрицю краще записати без множника попереду.
Зауваження.При знаходженні зворотної матриці доводиться виконувати досить багато обчислень і незвичайно правило розміщення додатків алгебри в підсумковій матриці. Тому велика ймовірність помилки. Щоб уникнути помилок, слід робити перевірку: обчислити твір вихідної матриці на підсумкову в тому чи іншому порядку. Якщо в результаті вийде одинична матриця, зворотна матриця знайдена правильно. Інакше потрібно шукати помилку.
приклад.Знайдіть зворотну матрицю для матриці 
.
Рішення.
- Існує.
Відповідь: 
.
Висновок.Знаходження зворотної матриці за формулою (1) потребує забагато обчислень. Для матриць четвертого порядку та вище це неприйнятно. Реальний алгоритм знаходження зворотної матриці буде наведено пізніше.
Обчислення визначника та зворотної матриці за допомогою методу Гауса
Метод Гауса можна використовувати для знаходження визначника та зворотної матриці.
Саме, визначник матриці дорівнює det.
Зворотна матриця є рішенням систем лінійних рівнянь шляхом виключення Гауса:
Де є j-ий стовпець одиничної матриці - шуканий вектор.
Отримані вектори рішень - утворюють, очевидно, стовпці матриці , оскільки .
Формули для визначника
1.
Якщо матриця невироджена, то (твор провідних елементів).
Обчислення визначників n-го порядку:
Поняття визначника n-го порядку
Користуючись цією статтею про визначників, ви обов'язково навчитеся вирішувати завдання на кшталт наступного:
Розв'язати рівняння:
та багатьох інших, які так люблять вигадувати викладачі.
Визначник матриці або просто визначник грає важливу роль у вирішенні систем лінійних рівнянь. Загалом визначники і були придумані для цієї мети. Оскільки часто кажуть також "визначник матриці", згадаємо тут і матриці. Матриця- Це прямокутна таблиця, складена з чисел, які не можна міняти місцями. Квадратна матриця - таблиця, у якій число рядків та число стовпців однаково. Визначник може бути лише у квадратної матриці.
Зрозуміти логіку запису визначників легко за наступною схемою. Візьмемо знайому вам зі шкільної лави систему із двох рівнянь із двома невідомими:
У визначнику послідовно записуються коефіцієнти за невідомих: у першому рядку - з першого рівняння, у другому рядку - з другого рівняння:
Наприклад, якщо дана система рівнянь
то з коефіцієнтів при невідомих формується наступний визначник:
Отже, нехай дана квадратна таблиця, що складається з чисел, розташованих у nрядках (горизонтальних рядах) та в nстовпчиках (вертикальних рядах). За допомогою цих чисел за деякими правилами, які ми вивчимо нижче, знаходять число, яке називають визначником n-го порядку і позначають так:
(1)
Числа називають елементамивизначника (1) (перший індекс означає номер рядка, другий – номер стовпця, на перетині яких стоїть елемент; i = 1, 2, ..., n; j= 1, 2, …, n). Порядок визначника – це його рядків і стовпців.
Уявна пряма, що з'єднує елементи визначника, які обидва індексу однакові, тобто. елементи
називається головною діагоналлю, інша діагональ – побічний.
Обчислення визначників другого та третього порядків
Покажемо, як обчислюються визначники перших трьох порядків.
Визначник першого порядку – це елемент тобто.
Визначник другого порядку є число, яке отримується таким чином:
, (2)
Добуток елементів, що стоять відповідно на головній та на побічній діагоналях.
Рівність (2) показує, що зі своїм знаком береться добуток елементів головної діагоналі, а з протилежним – добуток елементів побічної діагоналі
.
приклад 1.Обчислити визначники другого порядку:
Рішення. За формулою (2) знаходимо:
Визначник третього порядку – це число, яке отримується так:
(3)
Запам'ятати цю формулу важко. Однак існує просте правило, зване правилом трикутників
, що дозволяє легко відтворити вираз (3). Позначаючи елементи визначника точками, з'єднаємо відрізками прямої ті з них, які дають добуток елементів визначника (рис. 1).
Формула (3) показує, що зі своїми знаками беруться добутки елементів головної діагоналі, а також елементів, розташованих у вершинах двох трикутників, основи яких їй є паралельними; із протилежними – твори елементів побічної діагоналі, а також елементів, розташованих у вершинах двох трикутників, які їй паралельні
.
На рис.1 головна діагональ та відповідні їй основи трикутників та побічна діагональ та відповідні їй основи трикутників виділені червоним кольором.
При обчисленні визначників дуже важливо, як і в середній школі, пам'ятати, що число зі знаком мінус, помножене на число зі знаком мінус, в результаті дає число зі знаком плюс, а число зі знаком плюс, помножене на число зі знаком мінус, в результаті дає число зі знаком мінус.
приклад 2.Обчислити визначник третього порядку:
Рішення. Користуючись правилом трикутників, отримаємо
Обчислення визначників n-го порядку
Розкладання визначника по рядку або стовпцю
Для обчислення визначника n-го порядку необхідно знати та використовувати наступну теорему.
Теорема Лапласа.Визначник дорівнює сумі творів елементів будь-якого рядка з їхньої алгебраїчні доповнення, тобто.
Визначення. Якщо у визначнику n-го порядку вибрати довільно pрядків та pстовпців ( p < n), то елементи, що знаходяться на перетині цих рядків та стовпців, утворюють матрицю порядку .
Визначник цієї матриці називається мінором
вихідного визначника. Наприклад, розглянемо визначник:
З рядків та стовпців з парними номерами збудуємо матрицю:
Визначник
називається міноромвизначника. Отримали мінор другого порядку. Ясно, що можна побудувати різні мінори першого, другого і третього порядку.
Якщо взяти елемент і викреслити в визначнику рядок і стовпець, на перетині яких він стоїть, отримаємо мінор, званий мінором елемента , який позначимо через :
.
Якщо мінор помножити на , де 3 + 2 – сума номерів рядка та стовпця, на перетині яких стоїть елемент, то отриманий твір називається алгебраїчним доповненнямелемента і позначається ,
Взагалі, мінор елемента будемо позначати , а додаток алгебри ,
(4)
Наприклад обчислимо алгебраїчні доповнення елементів та визначника третього порядку:
За формулою (4) отримаємо
При розкладанні визначника часто використовується така властивість визначника n-го порядку:
якщо до елементів будь-якого рядка чи стовпця додати добуток відповідних елементів іншого рядка чи стовпця на постійний множник, то значення визначника не зміниться.
Приклад 4.
Попередньо віднімемо з першого і третього рядків елементи четвертого рядка, тоді матимемо
У четвертому стовпці отриманого визначника три елементи – нулі. Тому вигідніше розкласти цей визначник за елементами четвертого стовпця, тому що три перші твори будуть нулями. Тому
Перевірити рішення можна за допомогою калькулятора визначників онлайн .
На наступному прикладі показано, як обчислення визначника будь-якого (у разі - четвертого) порядку можна звести до обчислення визначника другого порядку.
Приклад 5.Обчислити визначник:
Віднімемо з третього рядка елементи першого рядка, а до елементів четвертого рядка додамо елементи першого рядка, тоді матимемо
У першому стовпці всі елементи, крім першого, – нулі. Тобто визначник можна вже розкласти по першому стовпцю. Але нам не хочеться обчислювати визначник третього порядку. Тому зробимо ще перетворення: до елементів третього рядка додамо елементи другого рядка, помножені на 2, та якщо з елементів четвертого рядка віднімемо елементи другого рядка. В результаті визначник, що є додатком алгебри, сам може бути розкладений по першому стовпцю і нам залишиться тільки обчислити визначник другого порядку і не заплутатися в знаках:
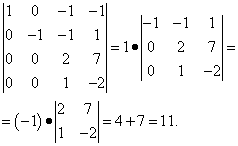
Приведення визначника до трикутного вигляду
Визначник, де всі елементи, що лежать з одного боку однієї з діагоналей, дорівнюють нулю, називається трикутним. Випадок побічної діагоналі шляхом зміни порядку рядків або стовпців на зворотний зводиться до нагоди головної діагоналі. Такий визначник дорівнює добутку елементів головної діагоналі.
Для приведення до трикутного вигляду використовується та сама властивість визначника n-го порядку, який ми застосовували у попередньому параграфі: якщо до елементів будь-якого рядка чи стовпця додати добуток відповідних елементів іншого рядка чи стовпця на постійний множник, то значення визначника не зміниться.
Перевірити рішення можна за допомогою калькулятора визначників онлайн .
Властивості визначника n-го порядку
У двох попередніх параграфах ми вже використовували одну з властивостей визначника n-го порядку. У деяких випадках для спрощення обчислення визначника можна скористатися іншими найважливішими властивостями визначника. Наприклад, можна привести визначник до суми двох визначників, з яких один або обидва можуть бути зручно розкладені по рядку або стовпцю. Випадків такого спрощення достатньо і вирішувати питання використання тієї чи іншої властивості визначника слід індивідуально.
