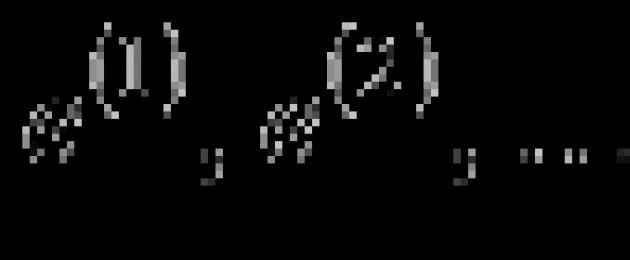Ако разглобим концепцията за n-светов вектор и въведем операции върху вектори, тогава те обясниха, че липсата на всички n-святови вектори при генерирането на линейно пространство. В тази статия ще говорим за най-важните причини за разбиране - разширяването и основата на векторното пространство. Също така, нека да разгледаме теоремата за разширяването на голям вектор зад базис и връзки между различни бази на n-святово пространство. Съобщава се, че анализираме решението на характерни приложения.
Навигация отстрани.
Концепцията за обхвата на векторното пространство и базиса.
Разбирането на разнообразието и основата на векторното пространство без междинно взаимодействие с понятията на линейно независимата векторна система се препоръчва, ако е необходимо, да се преобразува в състоянието на линейната грешка на векторната система, силата на линейната заблуда и независимостта.
Назначаване.
Отвореност на векторното пространствосе нарича числото, което е равно на максималния брой линейно независими вектори в това пространство.
Назначаване.
Основа на векторното пространство- последователността от линейно независими вектори в това пространство е подредена, като броят им е равен на изобилието на пространството.
Нека донесем някои дякони на mirkuvannya, излизайки от тези назначения.
Нека да разгледаме обхвата на n-святовите вектори.
Показано е, че разширяването на кое пространство е по-скъпо от n.
Вземете предвид система от n единични вектора
Приемаме q вектора и y реда на матрица A . І тук матрица A ще бъде единична матрица с размер n на n. Рангът на матрицата е по-скъп n (за необходимостта да се чудите на статията). Баща, система от вектори 
линейно независим, освен това е невъзможно да се добави желания вектор към системата, без да се разруши линейната независимост. Oskílki брой вектори в системата тогава едно n отвореност към пространството на n-светови вектори в ред n и единични вектори е основата на това пространство.
От остатъка от втвърдяването на това назначаване до основата е възможно да се направи visnovok, който е система от n-светови вектори, броят на векторите във всеки един е по-малък от n, а не база.
Сега можем да пренаредим първия и другия вектор на системата . Лесно е да се покаже, че системата от вектори е била 
е и основата на n-световното векторно пространство. Ние сгъваме матрицата, като вземаме нейните редове от векторни системи. Тази матрица може да бъде съкратена от една матрица чрез размяна на местата на първия и другите редове, също така нейният ранг е равен на n. По този начин, система от n вектора линейно независим и е основата на n-световното векторно пространство.
Как да пренаредите други вектори на системата , тогава се отнема още една основа.
Ако вземете линейно независима система от неединични вектори, тя също е основата на n-святово векторно пространство.
по такъв начин, Векторно пространство на разнообразие и n ma st_lki бази, skіlki іsnuє линейно независими системи от n n -световни вектори.
Ако говорим за двусветово векторно пространство (tobto, за равнина), тогава основата е два, ако не колинеарни, вектора. Основата на пространството на триви-света е три некомпланарни вектора.
Нека да разгледаме много приложения.
дупето.
Какъв е векторът и основата на пространството на триви-света?
Решение.
Doslіdzhuєmo tsyu система vektorіv на іnіynu zalezhіnі. За което сгъваме матрицата, чиито редове ще бъдат координатите на векторите и знаем ранга: 
В този ред векторите a, b и c са линейно независими и техният брой е равен на размера на векторното пространство, а смрадът е основата на това пространство.
Внушение:
Да, да
дупето.
Може ли векторна система да бъде основа на векторно пространство?
Решение.
Системата от вектори е линейно угар, но максималният брой линейно независими триизмерни вектори е три. Също така тази векторна система може да бъде основа на тривиално векторно пространство (ако подсистемата на векторна система е основа).
Внушение:
аз не мога
дупето.
Променете мнението си, какви вектори 
може да бъде основа на променливо векторно пространство.
Решение.
Нека добавим матрицата, като вземем нейните редове от изходни вектори: 
Ние знаем: 
По този начин системата от вектори a, b, c, d е линейно независима от това, че тяхната колкист dorіvnyuє razmіrnostі векторно пространство, също, a, b, c, d е th основа.
Внушение:
Vihіdnі вектори е основа chotirivimіrnogo простор.
дупето.
Chi да стане вектор и основа на векторното пространство 4?
Решение.
Navіt като vihіdna система от вектори е линейно независима, броят на векторите в нея не е достатъчен, за да бъде основата на chotirivimir пространство (базата на такова пространство се състои от 4 вектора).
Внушение:
Не, не сгъвай.
Разпределение на вектор върху базис на векторно пространство.
Нека имам няколко вектора е основата на n-световното векторно пространство. Ако добавим n-виртуален вектор x към тях, тогава системата от вектори ще бъде линейно оставена. От мощността на линейната угар знаем, че ако един вектор на линейната угарна система е линейно изразен през останалите. С други думи, ако един от векторите в линейната угарна система е разположен зад други вектори.
Така се доближихме до една важна теория.
Теорема.
Дали вектор от векторно пространство от n свят е разпределен в един ранг според основата.
Привеждане.
Хайде - Основа на n-световото векторно пространство. Допълним към tsikh vector_v n-светов вектор x. Тогава системата от вектори ще бъде линейно оставена и векторът x може да бъде линейно изразен чрез вектори. : de - deakі числа. Така че взехме оформлението на вектора x като основа. Загубено да донесе, scho rozladannya edine.
Допустимо е да има още едно оформление, де 
- Действителни числа. Вижда се от лявата и дясната част на оставащото равенство, видно е от лявата и дясната част на равенството:
Система от базисни вектори Оскилки е линейно независим, тогава поради обозначението на линейната независимост на системата от вектори, равенството е възможно само ако всички коефициенти са равни на нула. Този, който носи единството на разпределението на вектора според основата.
Назначаване.
Коефициентите се наричат координати на вектора x в базиса .
Тъй като сме запознати с теоремата за разпространението на вектора според основата, започваме да разбираме същността на „векторните задачи от n-свят“ 
". Tse означава, че разглеждаме вектора x на n-световото векторно пространство, координатите на всяка дадена задача в дадения базис. В най-доброто от нашите умове, че векторът x в друга основа на векторното пространство на n-света ще има координати, vіdminnі víd .
Нека да разгледаме тази задача.
Нека вземем система от n линейно независими вектора за даден базис на векторно пространство от n свят 
та вектор . Тоди вектори е и основата на това векторно пространство.
Нека знаем координатите на вектора x в основата . Значително q координати як .
Вектор x y основа може да е докладвано. Нека запишем равенството на координатната форма:
Tsya rіvnіst rіvnostrong systemі z n_linear rіvnіnі алгебра z n nevіdomimi zminnimi :
Вижда се основната матрица на системата 
Значително нейната буква A. Stovptsі матрици A е вектори на линейно независима система от вектори. Следователно, рангът на матрицата е равен на n , също така, нейният vyznachnik vídminny víd нула. Този факт показва, че системата може да бъде равна на едно решение, което може да бъде намерено по произволен метод, например или.
Така че ще намерите координатите вектор x y основа .
Нека анализираме теорията от приложения.
дупето.
В действителната основа на тривимерното векторно пространство, дадените вектори 
Помислете отново, че системата от вектори също е основата на това пространство и знае координатите на вектора x от тази основа.
Решение.
За да бъде системата от вектори в основата на едно тривиално пространство, беше необходимо тя да бъде линейно независима. Ясно е, че рангът на матрицата A се определя от редовете на векторите. Ранг, известен по метода на Гаус 
Освен това Rank(A) = 3, което показва линейната независимост на векторната система.
Отново векторът е основата. Нека има базисен вектор x maє координати. Тогава, както показахме повече, свързването на координатите на този вектор се дава от системата за изравняване 
Подчинявайки се на нея, обърнете внимание на смисъла, отнемете го 
Virishimo я метод на Cramer: 
По този начин векторът x в основата няма координати 
.
Внушение:
дупето.
На базата на deacom 
chotirivimir векторно пространство е дадена линейно независима система от вектори 
Видомо що 
. Намерете координатите на вектора x в основата .
Решение.
Oskílki векторна система 
линейно независима от ума, тя е в основата на четириривимирска шир. Todі rivnіst означава, че векторът x е в основата може да координира. Значително координатите на вектора x в основата як.
Системата за подравняване, която задава връзката на координатите на вектора x в бази і може да гледа 
Заменете в него дадените стойности и известни координати: 
Внушение:
.
Връзка между базите.
Нека даденият базис на n-световото векторно пространство задава две линейно независими векторни системи 
і
Tobto, вонята също е в основата на това пространство.
Якщо 
- координати на вектора в основата , след това връзката на координатите 
і зададен от системата от линейни линии (те говориха за нас в предната точка): 
, в матричната форма може да се запише като 
По подобен начин за вектор можем да напишем 
Предните матрични равенства могат да бъдат комбинирани в едно, което всъщност задава връзките на векторите в две различни бази. 
По подобен начин можем да изброим всички вектори и основата през основата 
:
Назначаване.
Матрица 
име преходна матрица към основа към основата дори тогава равенството е справедливо 
След умножаване на обидите, частите от цената на еквивалентността са десни
взета 
Познаваме преходната матрица, под която няма да докладваме за добре познатата опорна матрица и умножени матрици (удивете се на необходимостта от статистика): 
Загубени z'yasuvati zv'yazok векторни координати в дадените бази.
Тогава нека базисният вектор x има координати 
и основата е векторът x и координатите , тогава 
Останалите части на останалите две равенства са еднакви, можем да приравним десните части: 
Как да умножим обидите на десните части върху
тогава вземаме 
От другата страна 
(Запознайте се сами с обратната матрица).
Останалите две равенства ни дават списък от връзки на координатите на вектора x в бази i.
Внушение:
Преходната матрица от основа към основа може да се види 
;
координатите на вектора x в основите и свързани с 
или .
Разгледахме разбирането на разнообразието и основата на векторното пространство, научихме се как да оформяме вектора според основата и показахме връзката между различни бази на n-световното пространство на вектора чрез преходната матрица.
Страна 1
Pіdprostir, yogo основа и rozmirnіst.
Хайде Л- Линейно пространство над полето П і А- субкратни s Л. Якщо Азапазете редовото пространство над полето Пколко тихи са самите операции, какво Л, тогава Анаричаме подпространството на пространството Л.
Vіdpovіdno до назначаването на линейно пространство, shob Абеше необходимо пространството да преосмисли съществуването на Аоперации:
1) : 
;
2) 
: 
;
и проверете дали операциите в Аподреждане на осем аксиоми. Prote ще остане zayvim (заради факта, че аксиомите са написани на L) за вас. справедлива офанзива
Теорема.Нека L линейно пространство над полето P i 
. Безлични A todі і по-малко tоdі е pіdprostorom L, ако такива vimogi са победоносни:
1. : ;
2. : .
Твърдост.Якщо Л – н-спокойно линейно пространство, което Айога pіdprostіr, тогава Асъщо крайното линейно пространство и йога експанзията не надхвърлят н.
П 
пример 1. Chi е pіdprostorom пространство vectorіv-vіdrіzkіv V2 безличен S всички векториv област, skin z yah лежат на една от осите на координати 0x или 0y?
Решение: Хайде 
, 
і 
, 
. Тоди 
. Otzhe, S не е подпространство 
.
дупе 2. V 2 vectorіv-vіdrіzkіv равнина без лич Свсички вектори в равнината, на кочана и кинци от тези лежат на тази права линия лкаква област?
Решение.
д 
sli вектор 
умножете по число к, тогава вземаме вектора 
, също лежат С. Якшчо 
і 
са два вектора от S, тогава 
(следвайки правилото за сгъване на вектори върху права линия). Otzhe, S є pіdprostorom 
.
Пример 3. Chi е линейно подпространство на линейно пространство V 2 безличен Ана всички вектори в равнината л, (Да приемем, че кочанът на всеки вектор се zbígaêtsya с кочана на координатите)?
Р 
решение.
На моменти, ако е прав лне преминават през кочана от координати НОлинейно подпространство V 2
не е, защото 
.
На моменти, ако е прав л
преминава през кочана от координати, без лице НОе линейно подпространство V 2
,
защото 
i при множител на всеки вектор 
номер на циферблата α
от полето Рвзета 
. В този ранг, в допълнение към линейното пространство за множество НОвиконани.
Пример 4.Нека системата от вектори е дадена 
от линейното пространство Лнад полето П. Да се докаже, че няма различни линейни комбинации 
с коефициенти 
ч Пе подпространство Л(ce pіdprosіr Анаречено подпространство, генерирано от системата от вектори или линейна обвивка векторни системи, и означете така: 
или 
).
Решение. Вярно, до това, тогава за каквито и да е елементи х,
г
Аможе би: 
, 
, де 
, 
. Тоди
така як , тогава 
към това 
.
Нека преразгледаме валидността на друга мисъл за теоремата. Якщо х- бъдете вектор Аі T- било то число z П, тогава. Оскилки 
і 
,, тогава 
, към това 
. В този ред, zgіdno z теореми, безлични А- Разширение на линейното пространство Л.
За последните линейни пространства е справедливо и обратимо.
Теорема. Be-yaky pіdprostіr НОлинейно пространство Лнад полето 
е линейна обвивка на пеещата система от вектори.
Когато razv'yazannі проблем znakhodzhennya основа и razmіrnostі linіynoї okolonka vikoristovuyu дойде теорема.
Теорема.Основа на линейна обвивка 
работа с основата на векторната система . Разширяване на линейния корпус варира с ранга на векторната система .
Пример 4.Познайте основата и разширяването на пространството 
линейно пространство Р 3
[
х]
, като 
, 
, 
, 
.
Решение. Vіdomo, scho вектори и техните координатни редове (stovptsі) могат да имат една и съща мощност (показват линейни угар). Добавяне на матрица А=
от координатни вектори 
в основата 
.
Знаем ранга на матрицата А.
. М 3
=
. 
.
Баща, ранг r(А)=
3. Също така, рангът на система от вектори още 3. По-късно разширението на подпространството S е повече от 3, като основата е съставена от три вектора 
(защото в основен минор 
въведете координатите на тези вектори)., . Tsya векторна система е линейно независима. Добре, хайде.
І 
.
Можете да преразгледате каква е системата 
линейно угар за всеки вектор хч з. Cim донесе шо 
максимална линейно независима система от вектори в подпространството з, тогава. - основа y з ta dim з=н 2
.
страна 1
Линейно пространство V се нарича n-миркато в нова система система от n линейно независими вектора и дали система с по-голям брой вектори е линейно независима. Числото n се нарича rozmirnistyu (брой vimiriv)означава се линейно пространство V i \име на оператора(dim)V. С други думи, разширяването на пространството е максималния брой линейно независими вектори в това пространство. Като такъв kіlkіst іsnuє, тогава просторът се нарича kіtsev. Ако за всяко естествено число n пространството V има система, която е съставена от n линейно независими вектора, тогава такова пространство се нарича неизчерпаемо (запишете: \име на оператора(dim)V=\infty). Далеч, сякаш не мъдро враждебни, ще гледат просторите на края.
Основа n-световно линейно пространство се нарича подредена колекция от n линейно независими вектора ( базисни вектори).
Теорема 8.1 за разлагането на вектор зад базис. Ако това е основата на n-святово линейно пространство V , тогава всеки вектор \mathbf(v)\in V може да има представяния в линейна комбинация от основни вектори:
\mathbf(v)=\mathbf(v)_1\cdot \mathbf(e)_1+\mathbf(v)_2\cdot \mathbf(e)_2+\ldots+\mathbf(v)_n\cdot \mathbf(e)_n
и пред същия ранг, tobto. коефициент \mathbf(v)_1, \mathbf(v)_2,\ldots, \mathbf(v)_nизпъкват ясно.С други думи, независимо дали има вектор в пространството, може да има подредби според основата и до същия ранг.
Вярно е, че отвореността към пространството V dorívnyuê n. Векторна система \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_nлинейно независими (базис ce). След като стигнем до основата на който и да е вектор \mathbf(v), можем да вземем линейна угарна система \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n, \mathbf(v)(Скалите на тази система са съставени от (n + 1) вектора в n-световното пространство). В името на 7 линейно оставени и линейно независими вектора можем да вземем броя на теоремите.
Последно 1. Якщо \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_nе база за пространството V , тогава V=\име на оператор(Lin) (\mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_n), тогава. Линейното пространство е линейната обвивка на основните вектори.
Вярно, за доказване на еквивалентност V=\operatorname(Lin) (\mathbf(e)_1,\mathbf(e)_2, \ldots, \mathbf(e)_n)две дузини dosit показват, че сте включени V\subset \operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_n)и те се включват веднага. Всъщност, от една страна, било то линейна комбинация от вектори в линейното пространство да лежи върху самото линейно пространство, т.е. \operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n)\подмножество V. От друга страна, тогава дали някакво векторно пространство отвъд Теорема 8.1 е възможно като линейна комбинация от основни вектори. V\subset \operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n). Можете да видите невъзмутимостта на гледането на множествата.
Последни 2. Якщо \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- линейно независима система от вектори в линейно пространство V и дали вектор \mathbf(v)\in V може да има представяния в линейна комбинация (8.4): \mathbf(v)=v_1\mathbf(e)_1+ v_2\mathbf(e)_2+\ldots+v_n\mathbf(e)_n, тогава пространство V може да разшири n и системата \mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_nе йога основа.
Действително, пространството V има система от n линейно независими вектора, но дали системата е или не \mathbf(u)_1,\mathbf(u)_2,\ldots,\mathbf(u)_nс по-голям брой вектори (k>n) е линейно угар, фрагменти от кожни вектори от системата са линейно изразени чрез вектори \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n. да означава, \име на оператора(dim) V=nі \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- Основа V.
Теорема 8.2 как да разширим система от вектори до базис. Бъдете линейно независима система от k вектора в n-светово линейно пространство (1\leqslant k Вярно, нека бъде - линейно независима система от вектори в n-световното пространство V~(1\leqslant k Уважение 8.4 1. Основата на линейното пространство е нееднозначна. Например като \mathbf(e)_1,\mathbf(e)_2, \ldots, \mathbf(e)_nе база за пространството V , тогава системата от вектори \lambda \mathbf(e)_1,\lambda \mathbf(e)_2,\ldots,\lambda \mathbf(e)_nза каквото и да е \lambda\ne0 също е основата на V . Броят на основните вектори в различни основи на едно и също крайномерно пространство, очевидно, са едни и същи, оскаловете на един и същ брой богатство на пространството. 2. В някои отворени пространства, които често се използват в допълнения, една от възможните основи, най-практична от практическа гледна точка, се нарича стандартна. 3. Теорема 8.1 ни позволява да кажем, че базисът е реална система от елементи в линейно пространство, до това дали вектор в пространството е линейно изразен чрез базисните вектори. 4. Yakscho безличен \mathbb(L) е линейна обвивка \operatorname(Lin)(\mathbf(v)_1,\mathbf(v)_2,\ldots,\mathbf(v)_k), след това векторите \mathbf(v)_1,\mathbf(v)_2,\ldots,\mathbf(v)_kнаречени удовлетворяващи множители \mathbb(L) . Последното 1 от теорема 8.1 чрез равенство V=\име на оператор(Lin) (\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n)позволете ми да кажа, че основата е минимална система от utvoryuyuchihлинейно пространство V , така че е невъзможно да промените броя на удовлетворяващите (ако искате да видите един вектор от набора \mathbf(e)_1, \mathbf(e)_2,\ldots,\mathbf(e)_n) без увреждане на капитала V=\име на оператор(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n). 5. Теорема 8.2 ни позволява да кажем, че основата е максимална линейно независима система от векторилинейно пространство, фрагменти от основата - напълно линейно независима система от вектори и е невъзможно да се допълни с вектор, без да се загуби линейна независимост. 6. Последните 2 от теорема 8.1 да се коригират ръчно за значимостта на основата и размерността на линейното пространство. Не е правилно определени асистенти да вземат въз основа на назначението, а за себе си: линейна независима система \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_nвектор в линейно пространство се нарича базис, както ако вектор в пространство се върти линейно през вектори \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n. Броят на основните вектори определя разнообразието на пространството. Ще бъде очевидно, че обозначението е еквивалентно на посочване по-високо. Например, rozmіrnіst и основа за buttіv іnіynykh простори, razglyuṇuh vysche. 1. Нулевото линейно пространство \(\mathbf(o)\) не отмъщава за линейно независими вектори. Следователно, rozmіrnіst на това пространство е vvazhut равен на нула: \dim\(\mathbf(o)\)=0. Tsei prostіr няма основа. 2. Интервалите V_1,\,V_2,\,V_3 могат да бъдат разделени 1, 2, 3 по нормален начин. Наистина, дали ненулев вектор към пространството V_1 установява линейно независима система (раздел. точка 1. съблюдавайте 8.2) и дали два ненулеви вектора към пространството V_1 са колинеарни, т.е. линейни отлагания (разр. челно 8.1). Освен това \dim(V_1)=1 и основата на пространството V_1 е вектор. По подобен начин може да се твърди, че \dim(V_2)=2 и \dim(V_3)=3 . Базисът на пространството V_2 може да бъде два неколинеарни вектора, взети в еднакъв ред (единият от тях се разглежда от първия базисен вектор, другият - от другия). Основата на пространството V_3 са три некомпланарни (които не лежат в една и съща или успоредни равнини) вектора, взети в същия ред. Стандартният базис V_1 е един вектор \ vec (i) на линията. Стандартната основа за V_2 е основата \vec(i),\,\vec(j), която се образува от два взаимно перпендикулярни единични вектора в равнината. Стандартната основа за пространството V_3 е основата \vec(i),\,\vec(j),\,\vec(k), Сгъвания на три единични по двойки перпендикулярни вектора, които отговарят на правилната тройка 3. Пространство \mathbb(R)^n за отмъщение за не повече от n линейно независими вектора. Всъщност ние вземаме k колони \mathbb(R)^n и ги сгъваме в разширителна матрица n\пъти k. Ако k>n, тогава стойностите са линейно зависими от теорема 3.4 за ранга на матрица. Отже, \dim(\mathbb(R)^n)\leqslant n. В пространството \mathbb(R)^n не е важно да знаете линейно независими колони. Например колоните на една матрица \mathbf(e)_1=\begin(pmatrix)1\\0\\\vdots\\0\end(pmatrix)\!,\quad \mathbf(e)_2= \begin(pmatrix)0\\1\ \\vdots\\0\end(pmatrix)\!,\quad \ldots,\quad \mathbf(e)_n= \begin(pmatrix) 0\\0\\vdots\\1 \end(pmatrix)\ ! . линейно независими. Отже, \dim(\mathbb(R)^n)=n. Извиква се пространството \mathbb(R)^n n-световно речево аритметично пространство. Наборът от вектори се взема предвид от стандартния базис на пространството \mathbb(R)^n. По същия начин може да се твърди, че \dim(\mathbb(C)^n)=nкъм това се извиква \mathbb(C)^n n-свят комплексно аритметично пространство. 4. Предположение, че ако решението на хомогенната система Ax=o може да бъде обложено с един поглед x=C_1\varphi_1+C_2\varphi_2+\ldots+C_(n-r)\varphi_(n-r), де r=\име на оператор(rg)A, а \varphi_1,\varphi_2,\ldots,\varphi_(n-r)- фундаменталната система от решения. Отже, \(Ax=o\)=\име на оператор(Lin) (\varphi_1,\varphi_2,\ldots,\varphi_(n-r)), тогава. основата на пространственото \(Ax=0\) решение на хомогенна система е фундаменталното системно решение, а размерът на пространството \dim\(Ax=o\)=n-r de n е броят на нехомогенните, и r е рангът на матрицата на системата. 5. В пространството M_(2\times3) матрица на разширение 2\times3 можете да изберете 6 матрица: \begin(gathered)\mathbf(e)_1= \begin(pmatrix)1&0&0\\0&0&0\end(pmatrix)\!,\quad \mathbf(e)_2= \begin(pmatrix)0&1&0\\0&0&0\end( pmatrix)\!,\quad \mathbf(e)_3= \begin(pmatrix) 0&0&1\\0&0&0\end(pmatrix)\!,\hfill\\ \mathbf(e)_4= \begin(pmatrix) 0&0&0\\ 1&0&0 \end(pmatrix)\!,\quad \mathbf(e)_5= \begin(pmatrix)0&0&0\\0&1&0\end(pmatrix)\!,\quad \mathbf(e)_6= \begin(pmatrix)0&0&0 \\0&0&1\end(pmatrix)\!,\hfill \end(gathered) \alpha_1\cdot \mathbf(e)_1+\alpha_2\cdot \mathbf(e)_2+\alpha_3\cdot \mathbf(e)_3+ \alpha_4\cdot \mathbf(e)_4+\alpha_5\cdot \math \alpha_6\cdot \mathbf(e)_6= \begin(pmatrix)\alpha_1&\alpha_2&\alpha_3\\ \alpha_4&\alpha_5&\alpha_6\end(pmatrix) по-добра нулева матрица е по-малко за тривиална \alpha_1=\alpha_2= \ldots= \alpha_6=0. След прочитане на равенството (8.5) отдясно се установява, че скин-матрицата с M_(2\times3) в линеен ред се изразява чрез избраните 6 матрици, т.е. M_(2\times)= \operatorname(Lin) (\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_6). Отже, \dim(M_(2\times3))=2\cdot3=6, и матрици \mathbf(e)_1, \mathbf(e)_2,\ldots,\mathbf(e)_6е основа (стандарт) на това пространство. По същия начин може да се твърди, че \dim(M_(m\пъти n))=m\cdot n. 6. За всяко естествено n в пространството P(\mathbb(C)) богати членове с комплексни коефициенти, могат да се познават линейно независими елементи. Например богати термини \mathbf(e)_1=1, \mathbf(e)_2=z, \mathbf(e)_3=z^2,\,\ldots, \mathbf(e)_n=z^(n-1)линейно независими, фрагменти от линията a_1\cdot \mathbf(e)_1+a_2\cdot \mathbf(e)_2+\ldots+a_n\cdot \mathbf(e)_n= a_1+a_2z+\ldots+a_nz^(n-1) по-подобен на нулевия богат член (o(z)\equiv0) по-малък от тривиалния a_1=a_2=\ldots=a_n=0. Oskílki tsya система от богато дефинирани термини е линейно независима от всяко естествено число, пространството P(\mathbb(C)) не е ограничено. По същия начин работим за неизчерпаемото разширяване на пространството P(\mathbb(R)) с богати членове с ефективни коефициенти. Разширението P_n(\mathbb(R)) няма по-богато сегментирани стъпки, по-ниски n окончания. Наистина, вектори \mathbf(e)_1=1, \mathbf(e)_2=x, \mathbf(e)_3=x^2,\,\ldots, \mathbf(e)_(n+1)=x^nудовлетворяват (стандартната) основа на това пространство, така че смрадите са линейно независими и всеки полином в P_n(\mathbb(R)) може да бъде представен във визуално линейна комбинация от тези вектори: a_nx^n+\ldots+a_1x+a_0=a_0\cdot \mathbf(e)_1+a_1 \mathbf(e)_2+\ldots+a_n\cdot \mathbf(e)_(n+1)Приложете основите на линейните пространства
yakí линейно независими. Вярно, това е линейна комбинация
7. Диапазонът C(\mathbb(R)) от функции без прекъсване е безкрайно спокоен. Вярно, за всеки естествен n богат 1,x,x^2,\lточки, x^(n-1), Те се разглеждат като непрекъснати функции, установяващи линейно независими системи (прекрасна предна част).
В космоса T_(\omega)(\mathbb(R))тригонометрични биноми (честоти \omega\ne0 ) с ефективни коефициенти, базата удовлетворява мономи \mathbf(e)_1(t)=\sin\omega t,~\mathbf(e)_2(t)=\cos\omega t. Вонята е линейно независима, парчетата са същата ревност a\sin\omega t+b\cos\omega t\equiv0може би по-малко за тривиално настроение (a=b=0) . Било то функция на ума f(t)=a\sin\omega t+b\cos\omega tлинейно изразено чрез основите: f(t)=a\,\mathbf(e)_1(t)+b\,\mathbf(e)_2(t).
8. Разширението \mathbb(R)^X на действителни функции, присвоени на кратни на X, оставащи в областта на присвояване на X, може да бъде ограничено или неизчерпаемо. Ако X е kіntsevy множител, тогава пространството \mathbb(R)^X е kіntsev (например, X=\(1,2,\lточки,n\)). Ако X е безличен, тогава интервалът \mathbb(R)^X не е ограничен (например интервалът \mathbb(R)^N последователности).
9. В пространството \mathbb(R)^(+) дали числото \mathbf(e)_1 е положително, а не равно на единица, то може да бъде основа. Вземете например числото \mathbf(e)_1=2. Тогава дали числото r е положително може да се каже чрез \mathbf(e)_1. покажете от поглед \alpha\cdot \mathbf(e)_1\колония r=2^(\log_2r)=\log_2r\ast2=\alpha_1\ast \mathbf(e)_1, de \alpha_1=\log_2r. Също така, разширяването на което пространство е равно на 1, числото \mathbf(e)_1=2 е основата.
10. Хайде \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- Основата на речта линейно пространство V. Значително върху линейната скаларна функция V, използвайки:
\mathcal(E)_i(\mathbf(e)_j)=\begin(cases)1,&i=j,\\ 0,&i\ne j.\end(cases)
В този случай, поради линейността на функцията \mathcal(E)_i, за определен вектор е необходимо \mathcal(E)(\mathbf(v))=\sum_(j=1)^(n)v_j \mathcal(E)(\mathbf(e)_j)=v_i.
По-късно бяха присвоени n елемента (ковектори). \mathcal(E)_1, \mathcal(E)_2, \ldots, \mathcal(E)_nполучено до пространството V^(\ast) . Уведомете ни това \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_n- Основа V^(\ast).
Първо, нека покажем, че системата \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_nлинейно независими. Вярно, вземете линейна комбинация от тези вектори (\alpha_1 \mathcal(E)_1+\ldots+\alpha_n\mathcal(E)_n)(\mathbf(v))=което е равно на нулевата функция
\mathbf(o)(\mathbf(v))~~ (\mathbf(o)(\mathbf(v))=0~ \forall \mathbf(v)\in V)\колон~ \alpha_1\mathcal(E )_1(\mathbf(v))+\ldots+\alpha_n\mathcal(E)_n(\mathbf(v))= \mathbf(o)(\mathbf(v))=0~~\forall \mathbf(v )\във V.
Подчинявайки се на спокойствието на qiu \mathbf(v)=\mathbf(e)_i,~ i=1,\ldots,n, ние взимаме \alpha_1=\alpha_2\cdot= \alpha_n=0. Отце, системата от елементи \mathcal(E)_1,\mathcal(E)_2,\ldots,\mathcal(E)_nпространството V^(\ast) е линейно независимо, до това \alpha_1\mathcal(E)_1+\ldots+ \alpha_n\mathcal(E)_n =\mathbf(o)може би по-малко за тривиален вид.
По друг начин може да се покаже, че линейна функция f\in V^(\ast) може да се види от линейна комбинация от ковектори \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_n. Deisno, за какъвто и вектор \mathbf(v)=v_1 \mathbf(e)_1+v_2 \mathbf(e)_2+\ldots+v_n \mathbf(e)_nчрез линейността на функцията f можем да вземем:
\begin(aligned)f(\mathbf(v))&= f(v_1 \mathbf(e)_1+\ldots+v_n \mathbf(e)_n)= v_1 f(\mathbf(e)_1)+\ldots+ v_n f(\mathbf(e)_n)= f(\mathbf(e)_1)\mathcal(E)_1(\mathbf(v))+ \ldots+ f(\mathbf(e)_n)\mathcal(E) _n (\mathbf(v))=\\ &=(f(\mathbf(e)_1)\mathcal(E)_1+\ldots+ f(\mathbf(e)_n)\mathcal(E)_n)(\mathbf ( v))= (\beta_1\mathcal(E)_1+ \ldots+\beta_n\mathcal(E)_n) (\mathbf(v)),\end(подравнено)
тобто. функцията f е представена като линейна комбинация f=\beta_1 \mathcal(E)_1+\ldots+\beta_n\mathcal(E)_nфункции \mathcal(E)_1,\mathcal(E)_2,\ldots, \mathcal(E)_n(числа \beta_i=f(\mathbf(e)_i)- Коефициенти на линейна комбинация). Otze, системата от ковектори \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_nе основата на полученото пространство V^(\ast) i \dim(V^(\ast))=\dim(V)(За последното пространство V).
Как да отбележите помилване, помилване на приятел или предложения, напишете в коментарите.
Системи от линейни равномерни линии
Настройка на проблема. Познайте основата и обозначете разширяването на линейното пространство на решението на системата
Планът на rozvyazannya.
1. Запишете матрицата на системата:
И с помощта на елементарни трансформации можем да преработим матрицата във форма на трико, т.е. към такъв изглед, ако всички елементи, които се намират под диагонала на главата, са равни на нула. Рангът на матрицата на системата е равен на броя на линейно независимите редове, така че в нашия случай броят на редовете, в които липсват ненулеви елементи:
Отвореността към космоса е решение. Ако е така, тогава една хомогенна система може да има едно нулево решение, ако е така, тогава системата може да има безлично решение.
2. Избираме основните и безплатните. Vilni zminní е значителен. След това ще променим основните промени през лентите, отримвайки в такъв ранг окончателното решение на единната система от линейни трасета.
3. Записваме основата за пространството на решението на системата последователно една от най-големите променливи равни единици, в противен случай нула. Разширяването на линейното пространство е решението на системата за увеличаване на броя на векторите в основата.
Забележка. Преди елементарните трансформации на матрицата може да се добави:
1. умножение (rozpodіl) на ред с множител, vídminny víd нула;
2. добавяне към следващия ред на следващия ред, умножено по числото;
3. пермутация на редове от субдекуди;
4. Преработка 1–3 за stovptsіv (в моменти на rozvyazannya системи на линейни подравнявания, елементарната преработка на stovptsіv не се отменя).
Задача 3.Познайте основата и определете разширението на линейното пространство на решението на системата.
Записваме матрицата на системата и след помощта на елементарни трансформации тя се довежда до вид на тризъбец:
Скъпи тогава
- Във връзка с 0
- Google+ 0
- Добре 0
- Facebook 0
