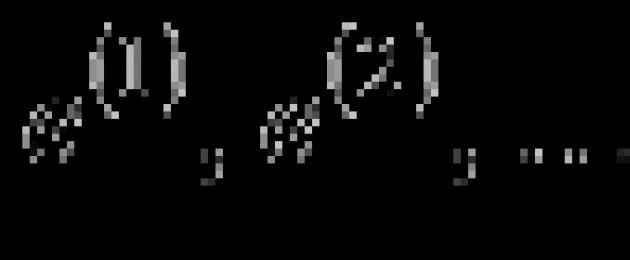Dacă am demontat conceptul de vector n lume și am introdus operații pe vectori, atunci ei au explicat că absența tuturor vectorilor n lume în generarea unui spațiu liniar. În acest articol, vom vorbi despre cele mai importante motive pentru înțelegere - extinderea și baza spațiului vectorial. Să ne uităm, de asemenea, la teorema despre răspândirea unui vector mare în spatele unei baze și a legăturilor dintre diferite baze ale unui spațiu n lume. Se pare că analizăm soluția aplicațiilor caracteristice.
Navigare pe lateral.
Conceptul domeniului de aplicare al spațiului vectorial și baza.
Înțelegerea diversității și a bazei spațiului vectorial fără interacțiune intermediară cu conceptele sistemului vectorial liniar independent, se recomandă ca, dacă este necesar, este necesar să se convertească la statutul de eroare liniară a sistemului vectorial, puterea erorii liniare și a independenței.
Programare.
Deschiderea spațiului vectorial se numește numărul, care este egal cu numărul maxim de vectori liniar independenți din acest spațiu.
Programare.
Baza spațiului vectorial- Tse a ordonat succesiunea de vectori liniar independenți din acest spațiu, numărul de astfel de spații liniare.
Să aducem câțiva diaconi ai mirkuvannya, ieșind din aceste întâlniri.
Să aruncăm o privire asupra domeniului de aplicare a vectorilor n-lumi.
Se arată că a cărui expansiune spațiul este mai scumpă decât n.
Luați în considerare un sistem de n vectori unici
Acceptăm q vectori și y rânduri ale matricei A . І aici matricea A va fi o singură matrice de expansiune n cu n. Rangul matricei este mai scump n (pentru nevoia de a te mira de articol). Părinte, sistem de vectori 
liniar independent, în plus, este imposibil să adăugați vectorul dorit la sistem fără a distruge independența liniară. Oskіlki numărul de vectori din sistem unul n, atunci deschiderea către spațiu a vectorilor n-lumi în ordinea n și a vectorilor unici є baza acestui spațiu.
De la restul întăririi acelei numiri până la bază, este posibil să se facă visnovok, care fi un sistem de n vectori lumi, numărul de vectori din oricare este mai mic decât n, nu o bază.
Acum putem rearanja primul și celălalt vector al sistemului . Este ușor de demonstrat că sistemul de vectori a fost 
este, de asemenea, baza spațiului vectorial n-lumi. Îndoim matricea, luând її rânduri de sisteme vectoriale. Această matrice poate fi trunchiată dintr-o singură matrice prin permutarea locurilor primului și altor rânduri, de asemenea, rangul її este egal cu n . Astfel, un sistem de n vectori liniar independent și є baza spațiului vectorial n-lumi.
Cum să rearanjați alți vectori ai sistemului , apoi mai este luată o bază.
Dacă luați un sistem liniar independent de vectori nu unici, acesta este, de asemenea, baza unui spațiu vectorial n-lumi.
Într-o asemenea manieră, Întinderea vectorială a diversității și n ma st_lki baze, skіlki іsnuє sisteme liniar independente din n n vectori din lume.
Dacă vorbim despre un spațiu vectorial cu două lumi (tobto, despre un plan), atunci baza este doi, dacă nu coliniari, vectori. Baza spațiului trivi-lumilor sunt trei vectori necoplanari.
Să aruncăm o privire la spratul de aplicații.
fundul.
Care este vectorul și baza spațiului trivi-lumilor?
Soluţie.
Doslіdzhuєmo tsyu system vektorіv pe іnіynu zalezhіnі. Pentru care îndoim matricea, ale cărei rânduri vor fi coordonatele vectorilor și cunoaștem rangul: 
În această ordine, vectorii a, b și c sunt independenți liniar, iar numărul lor este egal cu dimensiunea spațiului vectorial, iar mirosul este baza acestui spațiu.
Sugestie:
Da, y.
fundul.
Poate un sistem vectorial să fie baza unui spațiu vectorial?
Soluţie.
Sistemul de vectori este liniar liniar, dar numărul maxim de vectori tridimensionali liniar independenți este trei. De asemenea, acest sistem vectorial poate fi baza unui spațiu vectorial trivial (dacă subsistemul unui sistem vectorial este o bază).
Sugestie:
Nu pot.
fundul.
Răzgândește-te, ce vectori 
poate sta la baza unui spațiu vectorial variabil.
Soluţie.
Să adăugăm matricea, luând її rânduri de vectori de ieșire: 
Noi stim: 
Astfel, sistemul de vectori a, b, c, d este liniar independent de acel spațiu vectorial їх kolkіst dorіvnyuє razmіrnostі, de asemenea, a, b, c, d є baza.
Sugestie:
Vihіdnі vectori є bază chotirivimіrnogo întindere.
fundul.
Chi să devină vectorul și baza întinderii vectoriale a spațiului 4?
Soluţie.
Navіt ca sistem vihіdna de vectori este liniar independent, numărul de vectori din acesta nu este suficient pentru a fi baza unui spațiu chotirivimir (baza unui astfel de spațiu este alcătuită din 4 vectori).
Sugestie:
Nu, nu plia.
Distribuția unui vector pe baza spațiului vectorial.
Lasă-mă să am niște vectori є baza spațiului vectorial n-lumi. Dacă le adăugăm un vector n-virtual x, atunci sistemul de vectori va fi liniar îngrozit. Din puterea pârghiei liniare, știm că dacă un vector al sistemului liniar de pârghie este exprimat liniar prin ceilalți. Cu alte cuvinte, dacă unul dintre vectorii din sistemul liniar de pârghie este așezat în spatele altor vectori.
Astfel ne-am apropiat de o teorie importantă.
Teorema.
Dacă un vector al unui spațiu vectorial de n lume este distribuit într-un singur rang în funcție de bază.
Aducând.
Haide - Baza spațiului vectorial n-lumi. Dodamo la tsikh vector_v vector n-lume x. Apoi, sistemul de vectori va fi liniar îngrozit, iar vectorul x poate fi exprimat liniar prin vectori. : de - deakі numere. Deci am luat ca bază aspectul vectorului x. Pierdut de adus, scho rozladannya edine.
Este acceptabil să mai existe un aspect, de 
- Numerele reale. Poate fi văzut din părțile din stânga și din dreapta ale egalității rămase, este evident din părțile din stânga și din dreapta ale egalității:
Sistemul Oskilki de vectori de bază este liniar independentă, atunci datorită desemnării independenței liniare a sistemului de vectori, egalitatea este posibilă numai dacă toți coeficienții sunt egali cu zero. Cel care aduce unitatea distribuției vectorului după bază.
Programare.
Coeficienții se numesc coordonatele vectorului x din bază .
Deoarece suntem familiarizați cu teorema despre răspândirea unui vector în funcție de bază, începem să înțelegem esența „sarcinilor vectoriale n-lumi” 
". Tse înseamnă că luăm în considerare vectorul x al spațiului vectorial din n lume, coordonatele oricărei sarcini date în baza dată. În opinia noastră, că vectorul x într-o altă bază a spațiului vectorial n-lume va avea coordonate, vіdminnі vіd .
Să ne uităm la această sarcină.
Să luăm un sistem de n vectori liniar independenți pentru o bază dată a unui spațiu vectorial din n lume 
ta vector . Todi vectori є este și baza acestui spațiu vectorial.
Aflați-ne coordonatele vectorului x din bază . În mod semnificativ q coordonează iac .
Baza vector x y poate fi raportat. Să notăm egalitatea formei de coordonate:
Tsya rіvnіst rіvnostrong systemі z n_linear rіvnіnі algebra z n nevіdomimi zminnimi :
Se poate vedea matricea principală a sistemului 
Semnificativ її litera A. Stovptsі matrice A є vectori ai unui sistem de vectori liniar independent. Prin urmare, rangul matricei este egal cu n, de asemenea, її vyznachnik vіdminny vіd zero. Acest fapt indică faptul că sistemul poate fi egal cu o soluție, care poate fi găsită prin orice metodă, de exemplu, sau.
Deci veți găsi coordonatele baza vectoriala x y .
Să analizăm teoria din aplicații.
fundul.
În baza reală a spațiului vectorial trivimer, vectorii dați 
Să ne gândim că sistemul de vectori este și baza acestui spațiu și cunoaște coordonatele vectorului x din acea bază.
Soluţie.
Pentru ca sistemul de vectori să fie baza unui spațiu trivial, a fost necesar, astfel încât să fie liniar independent. Este clar că rangul matricei A este determinat de rândurile vectorilor. Rang cunoscut prin metoda Gauss 
De asemenea, Rank(A) = 3, care arată independența liniară a sistemului vectorial.
Din nou, vectorul este baza. Să aibă un vector de bază x coordonate maє. Apoi, după cum am arătat mai multe, legarea coordonatelor acestui vector este dată de sistemul de egalizare 
Supunându-te ei, minte sensul, ia-l 
Metoda lui Virishimo її Cramer: 
În acest fel, vectorul x din bază nu are coordonate 
.
Sugestie:
fundul.
La baza diacomului 
spatiului vectorial chotirivimir i se da un sistem de vectori liniar independent 
Vіdomo scho 
. Găsiți coordonatele vectorului x în bază .
Soluţie.
Sistem vectorial Oskіlki 
liniar independent de minte, ea sta la baza unei întinderi chotirivimir. Todі rivnіst înseamnă că vectorul x este în bază poate coordona. În mod semnificativ coordonatele vectorului x din bază iac.
Sistemul de aliniere, care stabilește legătura coordonatelor vectorului x în baze і poate vizualiza 
Înlocuiți în el valorile date și coordonatele cunoscute: 
Sugestie:
.
Legătura dintre baze.
Fie ca baza dată a spațiului vectorial din n lume să stabilească două sisteme vectoriale liniar independente 
і
Tobto, duhoarea stă și la baza acestei întinderi.
Yakscho 
- coordonatele vectorului de la bază , apoi legătura de coordonate 
і stabilite de sistemul de linii liniare (au vorbit despre noi în punctul din față): 
, în forma matriceală se poate scrie ca 
În mod similar pentru un vector, putem scrie 
Egalitățile matricei directe pot fi combinate într-una singură, care, de fapt, stabilește legăturile vectorilor în două baze diferite. 
În mod similar, putem enumera toți vectorii și baza prin baza 
:
Programare.
Matrice 
Nume matricea de tranziție la bază la baza chiar și atunci egalitatea este corectă 
După ce au înmulțit insultele, părțile din prețul echivalenței sunt dreptaci
Luat 
Cunoaștem matricea de tranziție, sub care nu vom raporta despre binecunoscuta matrice pivot și matrice înmulțită (ne minuneți de nevoia de statistici): 
S-au pierdut coordonatele vectoriale z'yasuvati zv'yazok în bazele date.
Fie ca vectorul de bază x să aibă coordonate, atunci 
iar baza este vectorul x și coordonatele , atunci 
Părțile rămase ale celor două egalități rămase sunt aceleași, putem echivala părțile potrivite: 
Cum să înmulțim insultele părților dreptaci pe
apoi luăm 
Din partea cealaltă 
(Cunoașteți singur matricea inversă).
Cele două egalități rămase ne oferă o listă de legături ale coordonatelor vectorului x în bazele i .
Sugestie:
Matricea de tranziție de la bază la bază poate fi vizualizată 
;
coordonatele vectorului x în baze și legate cu 
sau .
Ne-am uitat la înțelegerea diversității și a bazei spațiului vectorial, am învățat cum să așezăm vectorul în funcție de bază și am arătat legătura dintre diferitele baze ale spațiului n lume al vectorului prin matricea de tranziție.
Partea 1
Pіdprostir, baza yogo și rozmirnіst.
Haide L- Spațiu liniar deasupra câmpului P і A- submultiplu s L. Yakscho A stocați spațiul liniei deasupra câmpului P cât de liniștite sunt operațiunile în sine, ce L, apoi A numiți subspațiul spațiului L.
Vіdpovіdno până la numirea spațiului liniar, shob A a fost necesar ca spațiul să reconsidere existența A operatii:
1) : 
;
2) 
: 
;
și verificați dacă operațiunile din A ordonând opt axiome. Prote va rămâne zayvim (pentru faptul că axiomele sunt scrise cu L) pentru tine. ofensivă corectă
Teorema. Fie L spațiu drept peste câmpul P i 
. Impersonal A todі і less tоdі є pіdprostorom L, dacă astfel de vimogi sunt victorioși:
1. : ;
2. : .
Fermitate. Yakscho L – n-spaţiu liniar paşnic care A yoga pіdprostіr, atunci A de asemenea, spațiul liniar final și expansiunea yoga nu transcend n.
P 
exemplu 1. Chi є pіdprostorom space vectorіv-vіdrіzkіv V2 impersonal S toată zona vectorіv, pielea z yah se află pe una dintre axele coordonatelor 0x sau 0y?
Soluţie: Haide 
, 
і 
, 
. Todi 
. Otzhe, S nu este un subspațiu 
.
fundul 2. V 2 vectorіv-vіdrіzkіv avion fără lich S toți vectorii din plan, pe cob și kіntsі ale acelor se află pe această linie dreaptă l ce zona?
Soluţie.
E 
vector sli 
inmultiti cu un numar k, apoi luăm vectorul 
, de asemenea, culca S. Yakshcho 
і 
sunt doi vectori din S, atunci 
(urmând regula de pliere a vectorilor pe o linie dreaptă). Otzhe, S є pіdprostorom 
.
Exemplul 3. Chi є subspațiu liniar al spațiului liniar V 2 fără chip A a tuturor vectorilor din plan l, (Să presupunem că stiuletul oricărui vector zbіgaєtsya cu cobul de coordonate)?
R 
soluţie.
Uneori, dacă este drept l nu trece prin cobul de coordonate DAR subspațiu liniar V 2
nu є, pentru că 
.
Uneori, dacă este drept l
trece prin cobul de coordonate, fără chip DARє subspațiu liniar V 2
,
deoarece 
i la multiplicatorul oricărui vector 
număr de pe cadran α
din câmp R Luat 
. În acest rang, în plus față de spațiul liniar pentru multiplicitate DAR vikonanі.
Exemplul 4. Să fie dat sistemul de vectori 
din spațiul liniar L peste câmp P. Pentru a aduce, că nu există combinații liniare diferite 
cu coeficienți 
h Pє subspațiu L(ce pіdprosіr A numit subspațiu, generat de sistemul de vectori sau înveliș liniar sisteme vectoriale, și notează astfel: 
sau 
).
Soluţie. Adevărat, atunci pentru orice elemente X,
y
A poate: 
, 
, de 
, 
. Todi
deci iac , apoi 
la asta 
.
Să reconsiderăm validitatea unei alte gândiri a teoremei. Yakscho X- fi un vector Aі t- fie că este un număr z P, apoi. Oskilki 
і 
,, apoi 
, la asta 
. În această ordine, zgіdno z teoreme, impersonale A- Întinderea spațiului liniar L.
Pentru ultimele spații liniare, este corect și reversibil.
Teorema. Be-yaky pіdprostіr DAR spațiu liniar L peste câmp 
є înveliș liniar al sistemului cântând de vectori.
Când razv'yazannі problema znakhodzhennya baza și razmіrnostі linіynoї okolonka vikoristovuyu vin teorema.
Teorema. Baza unei învelișuri liniare 
lucrați cu baza sistemului vectorial . Extinderea carcasei liniare fluctuează cu rangul sistemului vectorial .
Exemplul 4. Cunoașteți baza și extinderea spațiului 
spațiu liniar R 3
[
X]
, ca 
, 
, 
, 
.
Soluţie. Vіdomo, vectorii scho și їх rândurile de coordonate (stovptsі) pot avea aceeași putere (afișează liniarul liniar). Adăugarea unei matrice A=
din vectori de coordonate 
la baza 
.
Cunoaștem rangul matricei A.
. M 3
=
. 
.
Părinte, rang r(A)=
3. De asemenea, rangul unui sistem de vectori mai mult 3. Mai târziu, expansiunea subspațiului S este mai mult 3, așa cum baza este compusă din trei vectori 
(pentru că la minor de bază 
introduceți coordonatele acestor vectori)., . Sistemul vectorial Tsya este liniar independent. Corect, haide.
І 
.
Puteți reconsidera ceea ce este sistemul 
liniar îngrozitor pentru orice vector X h H. Cim a adus sho 
sistem maxim liniar independent de vectori în subspațiu H, apoi. - baza y H ta dim H=n 2
.
partea 1
Spațiul liniar V se numește n-pace ca într-un sistem nou, un sistem de n vectori liniar independenți și dacă un sistem cu un număr mai mare de vectori este liniar independent. Se numește numărul n rozmirnistyu (numărul de vimiriv) se semnifică spaţiul liniar V i \operatorname(dim)V. Cu alte cuvinte, expansiunea spațiului este numărul maxim de vectori liniar independenți din acest spațiu. Ca un astfel de kіlkіst іsnuє, atunci întinderea se numește kіtsev. Dacă, pentru orice număr natural n, spațiul V are un sistem care este compus din n vectori liniar independenți, atunci un astfel de spațiu se numește inepuizabil (scrieți: \operatorname(dim)V=\infty). Departe, parcă nu sunt ostili cu înțelepciune, se vor uita la întinderile sfârșitului.
BazăÎntinderea liniară a n lume se numește o colecție ordonată de n vectori liniar independenți ( vectori de bază).
Teorema 8.1 despre expansiunea unui vector în spatele unei baze. Dacă este baza unui spațiu liniar de n lume V , atunci orice vector \mathbf(v)\în V poate avea reprezentări într-o combinație liniară de vectori de bază:
\mathbf(v)=\mathbf(v)_1\cdot \mathbf(e)_1+\mathbf(v)_2\cdot \mathbf(e)_2+\ldots+\mathbf(v)_n\cdot \mathbf(e)_n
iar inainte de acelasi rang, tobto. coeficient \mathbf(v)_1, \mathbf(v)_2,\ldots, \mathbf(v)_n iese în evidență clar. Cu alte cuvinte, indiferent dacă există un vector în spațiu, pot exista aranjamente în funcție de bază și până la același rang.
Adevărat, deschiderea către spațiu V dorіvnyuє n. Sistem vectorial \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n liniar independent (baza ce). După ce ajungem la baza oricărui vector \mathbf(v), putem lua un sistem liniar de pârghie \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n, \mathbf(v)(Scalele acestui sistem sunt compuse din (n + 1) vectori în spațiul n lume). De dragul a 7 vectori liniar liniar și independenți liniar, putem lua numărul de teoreme.
Ultimul 1. Yakscho \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n este o bază pentru spațiul V , atunci V=\operatorname(Lin) (\mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_n), apoi. Întinderea liniară este anvelopa liniară a vectorilor de bază.
Adevărat, pentru a dovedi echivalența V=\operatorname(Lin) (\mathbf(e)_1,\mathbf(e)_2, \ldots, \mathbf(e)_n) două duzini de doze arată că ești inclus V\subset\operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_n) iar ei intervin imediat. De fapt, dintr-o parte, fie că este o combinație liniară de vectori în spațiul liniar care să se afle pe spațiul liniar însuși, adică. \operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n)\subset V. Pe de altă parte, dacă orice spațiu vectorial dincolo de Teorema 8.1 este posibil ca o combinație liniară de vectori de bază, atunci. V\subset\operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n). Puteți vedea ecuanimitatea privirii la mulțimi.
Ultimele 2. Yakscho \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- un sistem liniar independent de vectori într-un spațiu liniar V și dacă un vector \mathbf(v)\în V poate avea reprezentări într-o combinație liniară (8.4): \mathbf(v)=v_1\mathbf(e)_1+ v_2\mathbf(e)_2+\ldots+v_n\mathbf(e)_n, atunci spațiul V poate extinde n și sistemul \mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_nє baza de yoga.
Într-adevăr, spațiul V are un sistem de n vectori liniar independenți, dar indiferent dacă sistemul este sau nu \mathbf(u)_1,\mathbf(u)_2,\ldots,\mathbf(u)_n cu un număr mai mare de vectori (k>n) este liniar îngrozit, cioburi de vectori de piele din sistem sunt exprimate liniar prin vectori \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n. A insemna, \operatorname(dim) V=nі \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- Baza V.
Teorema 8.2 cum se extinde un sistem de vectori la o bază. Fii un sistem liniar independent de k vectori într-un spațiu liniar de n lume (1\leqslant k Adevărat, să fie - un sistem liniar independent de vectori în întinderea n lume V~(1\leqslant k Respect 8.4 1. Baza spațiului liniar este ambiguă. De exemplu, ca \mathbf(e)_1,\mathbf(e)_2, \ldots, \mathbf(e)_n este o bază pentru spațiul V , apoi sistemul de vectori \lambda \mathbf(e)_1,\lambda \mathbf(e)_2,\ldots,\lambda \mathbf(e)_n pentru orice \lambda\ne0 este și baza lui V . Numărul de vectori de bază din baze diferite ale unuia și aceluiași spațiu finit-dimensional, evident, sunt aceiași, oscallurile aceluiași număr de bogăție de spațiu. 2. În unele spații deschise, care sunt adesea folosite în adăugiri, una dintre bazele posibile, cea mai practică din punct de vedere practic, se numește standard. 3. Teorema 8.1 ne permite să spunem că o bază este un sistem real de elemente într-un spațiu liniar, până la aceea, oricare spațiu vectorial este exprimat liniar prin vectorii de bază. 4. Yakscho impersonal \mathbb(L) є coajă liniară \operatorname(Lin)(\mathbf(v)_1,\mathbf(v)_2,\ldots,\mathbf(v)_k), apoi vectorii \mathbf(v)_1,\mathbf(v)_2,\ldots,\mathbf(v)_k numiți multiplicatori satisfăcători \mathbb(L) . Ultimul 1 din teorema 8.1 prin egalitate V=\operatorname(Lin) (\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n) permiteți-mi să spun că baza este sistem minim de utvoryuyuchih spațiu liniar V , astfel încât este imposibil să se schimbe numărul celor satisfăcători (dacă doriți să vedeți un vector din mulțime \mathbf(e)_1, \mathbf(e)_2,\ldots,\mathbf(e)_n) fără prejudiciu capitalului propriu V=\operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n). 5. Teorema 8.2 ne permite să spunem că baza este sistem maximal liniar independent de vectori spațiu liniar, cioburi de bază - un sistem de vectori complet independent liniar și este imposibil să îl completați cu un vector fără a pierde independența liniară. 6. Ultimele 2 din teorema 8.1 pentru a stabili manual semnificația bazei și dimensionalitatea spațiului liniar. Nu este corect ca anumiți asistenți să ia în baza programării, ci pentru ei înșiși: sistem liniar independent \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n un vector dintr-un spațiu liniar se numește bază, deci dacă un vector dintr-un spațiu este rotit liniar prin vectori sau nu \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n. Numărul de vectori de bază determină diversitatea spațiului. Va fi evident că desemnarea este echivalentă cu arătarea mai sus. De exemplu, baza rozmіrnіst i pentru întinderile buttіv іnіynykh, razglyuṇuh vysche. 1. Spațiul liniar zero \(\mathbf(o)\) nu răzbună vectorii liniar independenți. Prin urmare, rozmіrnіstul acestei întinderi este vvazhut egal cu zero: \dim\(\mathbf(o)\)=0. Tsei prostіr nicio bază. 2. Spațiile V_1,\,V_2,\,V_3 pot fi separate 1, 2, 3 într-un mod normal. Într-adevăr, dacă un vector diferit de zero la spațiul V_1 stabilește un sistem liniar independent (punctul div. 1. respect 8.2), și dacă doi vectori nenuli ai spațiului V_1 sunt coliniari, adică. depozite liniare (div. cap 8.1). De asemenea, \dim(V_1)=1 , iar baza spațiului V_1 este un vector. În mod similar, se poate argumenta că \dim(V_2)=2 și \dim(V_3)=3 . Baza spațiului V_2 poate fi doi vectori necoliniari, luați în aceeași ordine (unul dintre ei este considerat de primul vector de bază, celălalt - de celălalt). Baza spațiului V_3 este trei vectori necoplanari (care nu se află în același plan sau în plan paralel), luați în aceeași ordine. Baza standard V_1 este un singur vector \ vec (i) pe linie. Baza standard pentru V_2 este baza \vec(i),\,\vec(j), care este format din doi vectori individuali reciproc perpendiculari în plan. Baza standard pentru spațiul V_3 este baza \vec(i),\,\vec(j),\,\vec(k), Pliri a trei vectori perpendiculari uni perechi, care satisfac triplul drept 3. Spațiu \mathbb(R)^n pentru a răzbuna nu mai mult de n vectori liniar independenți. De fapt, luăm k coloane \mathbb(R)^n și le îndoim într-o matrice de expansiune de n\ ori k . Dacă k>n, atunci valorile sunt dependente liniar de teorema 3.4 despre rangul unei matrice. Otzhe, \dim(\mathbb(R)^n)\leqslant n. În spațiul \mathbb(R)^n nu este important să cunoaștem coloanele liniar independente. De exemplu, coloanele unei singure matrice \mathbf(e)_1=\begin(pmatrix)1\\0\\\vdots\\0\end(pmatrix)\!,\quad \mathbf(e)_2= \begin(pmatrix)0\\1\ \\vdots\\0\end(pmatrix)\!,\quad \ldots,\quad \mathbf(e)_n= \begin(pmatrix) 0\\0\\vdots\\1 \end(pmatrix)\ ! . liniar independent. Otzhe, \dim(\mathbb(R)^n)=n. Se numește spațiul \mathbb(R)^n spațiu aritmetic al vorbirii n-lume. Mulțimea vectorilor este luată în considerare de baza standard a spațiului \mathbb(R)^n. În mod similar, se poate argumenta că \dim(\mathbb(C)^n)=n la care se numește \mathbb(C)^n spatiu aritmetic complex din n lume. 4. Ghicind că dacă soluția sistemului omogen Ax=o poate fi taxată dintr-o privire x=C_1\varphi_1+C_2\varphi_2+\ldots+C_(n-r)\varphi_(n-r), de r=\operatorname(rg)A, A \varphi_1,\varphi_2,\ldots,\varphi_(n-r)- sistemul fundamental de soluţii. Otzhe, \(Ax=o\)=\operatorname(Lin) (\varphi_1,\varphi_2,\ldots,\varphi_(n-r)), apoi. baza soluției spațiale \(Ax=0\) a unui sistem omogen este soluția fundamentală a sistemului, iar dimensiunea spațiului \dim\(Ax=o\)=n-r de n este numărul celor neomogene și r este rangul matricei sistemului. 5. În matricea spațiului M_(2\times3) de expansiune 2\times3, puteți selecta 6 matrice: \begin(gathered)\mathbf(e)_1= \begin(pmatrix)1&0&0\\0&0&0\end(pmatrix)\!,\quad \mathbf(e)_2= \begin(pmatrix)0&1&0\\0&0&0\end( pmatrix)\!,\quad \mathbf(e)_3= \begin(pmatrix) 0&0&1\\0&0&0\end(pmatrix)\!,\hfill\\ \mathbf(e)_4= \begin(pmatrix) 0&0&0\\ 1&0&0 \end(pmatrix)\!,\quad \mathbf(e)_5= \begin(pmatrix)0&0&0\\0&1&0\end(pmatrix)\!,\quad \mathbf(e)_6= \begin(pmatrix)0&0&0 \\0&0&1\end(pmatrix)\!,\hfill \end(gathered) \alpha_1\cdot \mathbf(e)_1+\alpha_2\cdot \mathbf(e)_2+\alpha_3\cdot \mathbf(e)_3+ \alpha_4\cdot \mathbf(e)_4+\alpha_5\cdot \math \alpha_6\cdot \mathbf(e)_6= \begin(pmatrix)\alpha_1&\alpha_2&\alpha_3\\ \alpha_4&\alpha_5&\alpha_6\end(pmatrix) o matrice zero mai bună este mai mică pentru una trivială \alpha_1=\alpha_2= \ldots= \alpha_6=0. Citind egalitatea (8.5) din dreapta, se stabilește că matricea pielii cu M_(2\times3) într-o ordine liniară este exprimată prin cele 6 matrice selectate, adică. M_(2\times)= \operatorname(Lin) (\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_6). Otzhe, \dim(M_(2\times3))=2\cdot3=6, și matrice \mathbf(e)_1, \mathbf(e)_2,\ldots,\mathbf(e)_6є baza (standard) a acestui spațiu. În mod similar, se poate argumenta că \dim(M_(m\times n))=m\cdot n. 6. Pentru orice n natural din spațiul P(\mathbb(C)) termeni bogați cu coeficienți complecși, se pot cunoaște elemente liniar independente. De exemplu, termeni bogați \mathbf(e)_1=1, \mathbf(e)_2=z, \mathbf(e)_3=z^2,\,\ldots, \mathbf(e)_n=z^(n-1) liniar independente, cioburi de linie a_1\cdot \mathbf(e)_1+a_2\cdot \mathbf(e)_2+\ldots+a_n\cdot \mathbf(e)_n= a_1+a_2z+\ldots+a_nz^(n-1) mai asemănător cu termenul bogat zero (o(z)\equiv0) mai puțin decât cel banal a_1=a_2=\ldots=a_n=0. Sistemul Oskіlki tsya de termeni bogat definiți este liniar independent de orice număr natural, spațiul P(\mathbb(C)) nu este limitat. În același mod, se lucrează la expansiunea inepuizabilă a spațiului P(\mathbb(R)) cu termeni bogați cu coeficienți efectivi. Expansiunea P_n(\mathbb(R)) nu are pași mai bogat segmentați, n terminații inferioare. Într-adevăr, vectorii \mathbf(e)_1=1, \mathbf(e)_2=x, \mathbf(e)_3=x^2,\,\ldots, \mathbf(e)_(n+1)=x^n satisface baza (standard) a acestui spațiu, astfel încât puturosele sunt liniar independente și orice polinom din P_n(\mathbb(R)) poate fi reprezentat într-o combinație vizual liniară a acestor vectori: a_nx^n+\ldots+a_1x+a_0=a_0\cdot \mathbf(e)_1+a_1 \mathbf(e)_2+\ldots+a_n\cdot \mathbf(e)_(n+1)Aplicați elementele de bază ale spațiilor liniare
yakі liniar independent. Adevărat, aceasta este o combinație liniară
7. Intervalul C(\mathbb(R)) al funcțiilor fără întreruperi este infinit de pașnic. Adevărat, pentru orice natură bogată 1,x,x^2,\ldots, x^(n-1), Yaki sunt privite ca funcții neîntrerupte, care stabilesc sisteme liniar independente (fața minunată).
In spatiu T_(\omega)(\mathbb(R)) binoame trigonometrice (frecvențe \omega\ne0 ) cu coeficienți efectivi, baza satisface monomii \mathbf(e)_1(t)=\sin\omega t,~\mathbf(e)_2(t)=\cos\omega t. Duhoarea este liniar independentă, cioburile sunt aceeași gelozie a\sin\omega t+b\cos\omega t\equiv0 poate mai puțin pentru o dispoziție banală (a=b=0) . Fie că este o funcție a minții f(t)=a\sin\omega t+b\cos\omega t exprimat liniar prin baze: f(t)=a\,\mathbf(e)_1(t)+b\,\mathbf(e)_2(t).
8. Expansiunea \mathbb(R)^X a funcțiilor efective, alocate multiplilor lui X, aflate în spatele domeniului de atribuire a lui X poate fi finită sau inepuizabilă. Dacă X este un multiplicator kіntsevy, atunci spațiul \mathbb(R)^X este kіntsev (de exemplu, X=\(1,2,\ldots,n\)). Dacă X este impersonal, atunci spațiul \mathbb(R)^X nu este limitat (de exemplu, spațiul \mathbb(R)^N secvențe).
9. În spațiul \mathbb(R)^(+) dacă numărul \mathbf(e)_1 este pozitiv, nu egal cu unu, poate fi o bază. Luați, de exemplu, numărul \mathbf(e)_1=2. Dacă numărul r este într-un fel pozitiv poate fi spus prin \mathbf(e)_1 , atunci. arata la vedere \alpha\cdot \mathbf(e)_1\colon r=2^(\log_2r)=\log_2r\ast2=\alpha_1\ast \mathbf(e)_1, de \alpha_1=\log_2r. De asemenea, a cărui expansiune spațiu este egal cu 1, numărul \mathbf(e)_1=2 este baza.
10. Haide \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- Baza spațiului liniar de vorbire V. În mod semnificativ pe funcțiile scalare liniare V, folosind:
\mathcal(E)_i(\mathbf(e)_j)=\begin(cases)1,&i=j,\\ 0,&i\ne j.\end(cases)
În acest caz, datorită liniarității funcției \mathcal(E)_i, pentru un anumit vector este necesar \mathcal(E)(\mathbf(v))=\sum_(j=1)^(n)v_j \mathcal(E)(\mathbf(e)_j)=v_i.
Ulterior, au fost atribuite n elemente (covectori). \mathcal(E)_1, \mathcal(E)_2, \ldots, \mathcal(E)_n obţinut la spaţiul V^(\ast) . Spune-ne asta \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_n- Baza V^(\ast).
Mai întâi, să arătăm că sistemul \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_n liniar independent. Adevărat, luați o combinație liniară a acestor vectori (\alpha_1 \mathcal(E)_1+\ldots+\alpha_n\mathcal(E)_n)(\mathbf(v))= care este egal cu funcția nulă
\mathbf(o)(\mathbf(v))~~ (\mathbf(o)(\mathbf(v))=0~ \forall \mathbf(v)\in V)\colon~ \alpha_1\mathcal(E )_1(\mathbf(v))+\ldots+\alpha_n\mathcal(E)_n(\mathbf(v))= \mathbf(o)(\mathbf(v))=0~~\forall \mathbf(v) )\în V.
Supunerea la qiu equanimitate \mathbf(v)=\mathbf(e)_i,~ i=1,\ldots,n, luăm \alpha_1=\alpha_2\cdot= \alpha_n=0. Otze, sistemul de elemente \mathcal(E)_1,\mathcal(E)_2,\ldots,\mathcal(E)_n spațiul V^(\ast) este liniar independent de aceea \alpha_1\mathcal(E)_1+\ldots+ \alpha_n\mathcal(E)_n =\mathbf(o) poate mai puțin pentru o privire banală.
Într-un alt mod, se poate demonstra că o funcție liniară f\in V^(\ast) poate fi văzută dintr-o combinație liniară de covectori \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_n. Deisno, pentru orice vector \mathbf(v)=v_1 \mathbf(e)_1+v_2 \mathbf(e)_2+\ldots+v_n \mathbf(e)_n prin liniaritatea funcției f putem lua:
\begin(aligned)f(\mathbf(v))&= f(v_1 \mathbf(e)_1+\ldots+v_n \mathbf(e)_n)= v_1 f(\mathbf(e)_1)+\ldots+ v_n f(\mathbf(e)_n)= f(\mathbf(e)_1)\mathcal(E)_1(\mathbf(v))+ \ldots+ f(\mathbf(e)_n)\mathcal(E) _n (\mathbf(v))=\\ &=(f(\mathbf(e)_1)\mathcal(E)_1+\ldots+ f(\mathbf(e)_n)\mathcal(E)_n)(\mathbf ( v))= (\beta_1\mathcal(E)_1+ \ldots+\beta_n\mathcal(E)_n) (\mathbf(v)),\end(aligned)
tobto. funcția f este reprezentată ca o combinație liniară f=\beta_1 \mathcal(E)_1+\ldots+\beta_n\mathcal(E)_n funcții \mathcal(E)_1,\mathcal(E)_2,\ldots, \mathcal(E)_n(numerele \beta_i=f(\mathbf(e)_i)- Coeficienți de combinație liniară). Otze, sistemul covectorilor \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_nє baza spațiului rezultat V^(\ast) i \dim(V^(\ast))=\dim(V)(Pentru ultimul spațiu V).
Cum să comemorați o iertare, iertarea unui prieten sau propunerile, scrieți în comentarii.
Sisteme de linii liniare uniforme
Setarea problemei. Cunoașteți baza și semnificați extinderea spațiului liniar al soluției sistemului
Planul rozvyazannya.
1. Notați matricea sistemului:
Și cu ajutorul transformărilor elementare, putem reface matricea într-o formă de tricot, tobto. la o astfel de vedere, dacă toate elementele care sunt situate sub diagonala capului sunt egale cu zero. Rangul matricei sistemului este egal cu numărul de rânduri liniar independente, deci, în cazul nostru, numărul de rânduri, în care lipsesc elemente diferite de zero:
Deschiderea către spațiu este o soluție. Dacă da, atunci un sistem omogen poate avea o singură soluție zero, dacă da, atunci sistemul poate avea o soluție impersonală.
2. Le alegem pe cele de bază și pe cele gratuite. Vilni zminnі este semnificativă. Apoi, vom schimba modificările de bază prin benzi, otrimavshi într-un astfel de rang soluția finală a sistemului uniform de aliniamente liniare.
3. Scriem baza pentru spațiul soluției sistemului în succesiune una dintre cele mai mari unități egale modificabile, în caz contrar zero. Expansiunea spațiului liniar este soluția sistemului de a crește numărul de vectori din bază.
Notă. Înainte de transformările elementare ale matricei, se poate adăuga:
1. înmulțirea (rozpodіl) a unui rând cu un multiplicator, vіdminny vіd zero;
2. adăugarea la rândul următor al rândului următor, înmulțită cu numărul;
3. permutarea rândurilor de subdecude;
4. Reprelucrarea 1–3 pentru stovptsіv (în momentele sistemelor rozvyazannya de aliniamente liniare, reprelucrarea elementară a stovptsіv nu este vicorată).
Sarcina 3. Cunoașteți baza și determinați expansiunea spațiului liniar al soluției sistemului.
Notăm matricea sistemului și după ajutorul transformărilor elementare, este indus la un aspect de trident:
Dragă, atunci
- In contact cu 0
- Google+ 0
- O.K 0
- Facebook 0
