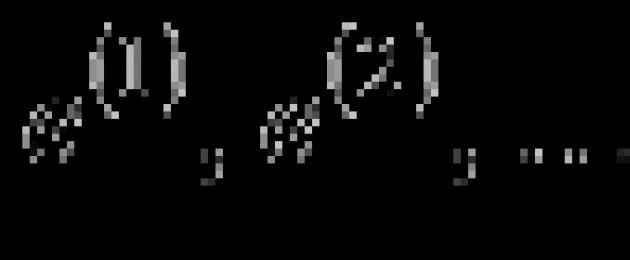Ak by sme rozobrali koncept n-svetového vektora a zaviedli operácie s vektormi, potom vysvetlili, že absencia všetkých n-svetových vektorov pri generovaní lineárneho priestoru. V tomto článku si povieme o najdôležitejších dôvodoch pochopenia – expanzii a základoch vektorového priestoru. Pozrime sa tiež na vetu o šírení veľkého vektora za bázou a väzbách medzi rôznymi bázami n-svetového priestoru. Údajne rozoberáme riešenie charakteristických aplikácií.
Navigácia na boku.
Pojem rozsahu vektorového priestoru a základ.
Pre pochopenie diverzity a základu vektorového priestoru bez intermediárnej súhry s konceptmi lineárne nezávislého vektorového systému sa odporúča, aby v prípade potreby bolo potrebné previesť do stavu lineárneho omylu vektorového systému, sila lineárneho omylu a nezávislosti.
Vymenovanie.
Otvorenosť vektorového priestoru volá sa číslo, ktoré sa rovná maximálnemu počtu lineárne nezávislých vektorov v tomto priestore.
Vymenovanie.
Základ vektorového priestoru- Tse usporiadal postupnosť lineárne nezávislých vektorov v tomto priestore, počet takýchto lineárnych priestorov.
Zoberme pár diakonov z mirkuvannya, ktorí odídu z týchto stretnutí.
Poďme sa pozrieť na rozsah n-svetových vektorov.
Ukazuje sa, že rozšírenie ktorého priestoru je drahšie ako n.
Vezmite do úvahy systém n jednotlivých vektorov
Akceptujeme q vektorov a y riadkov matice A . І tu matica A bude jedna matica s veľkosťou n x n. Hodnosť matice je drahšia n (pre potrebu čudovať sa článku). Otec, systém vektorov 
lineárne nezávislý, navyše nie je možné pridať požadovaný vektor do systému bez zničenia lineárnej nezávislosti. Oskіlki počet vektorov v systéme jeden n , teda otvorenosť priestoru n-svetových vektorov v poradí n a jednotlivých vektorov є základ tohto priestoru.
Zo zvyšku stvrdnutia toho vymenovania do základu je možné urobiť visnovok, ktorý byť systémom n-svetových vektorov, počet vektorov v ktoromkoľvek z nich je menší ako n, nie je základom.
Teraz môžeme zmeniť usporiadanie prvého a druhého vektora systému . Je ľahké ukázať, že systém vektorov bol 
je tiež základom n-svetového vektorového priestoru. Maticu zložíme, pričom vezmeme її riadky vektorových systémov. Táto matica môže byť skrátená z jednej matice permutáciou miest prvého a ďalších riadkov, tiež її poradie sa rovná n . Teda systém n vektorov lineárne nezávislý a є základ n-svetového vektorového priestoru.
Ako preusporiadať ostatné vektory systému , potom sa odoberie ešte jeden základ.
Ak vezmeme lineárne nezávislý systém nie jednotlivých vektorov, je to tiež základ n-svetového vektorového priestoru.
takýmto spôsobom, Vektorová rozloha diverzity a n ma st_lki báz, skіlki іsnuє lineárne nezávislé systémy od n n -svetových vektorov.
Ak hovoríme o dvojsvetovom vektorovom priestore (tobto, o rovine), tak základom sú dva, ak nie kolineárne, vektory. Základom priestoru trivi-sveta sú tri nekoplanárne vektory.
Poďme sa pozrieť na šprot aplikácií.
zadok.
Aký je vektor a základ priestoru trivi-sveta?
Riešenie.
Doslіdzhuєmo tsyu systém vektorіv na іnіynu zalezhіnі. Pre ktoré zložíme maticu, ktorej riadky budú súradnicami vektorov a poznáme poradie: 
V tomto poradí sú vektory a, b a c lineárne nezávislé a ich počet sa rovná veľkosti vektorového priestoru a základom tohto priestoru je smrad.
Návrh:
Áno, y.
zadok.
Môže byť vektorový systém základom vektorového priestoru?
Riešenie.
Systém vektorov je lineárne ladný, ale maximálny počet lineárne nezávislých trojrozmerných vektorov je tri. Tento vektorový systém môže byť tiež základom triviálneho vektorového priestoru (ak je základom podsystém vektorového systému).
Návrh:
nemôžem.
zadok.
Zmeňte názor, aký vektori 
môže byť základom variabilného vektorového priestoru.
Riešenie.
Pridajme maticu, keď vezmeme її riadky výstupných vektorov: 
Vieme: 
Systém vektorov a, b, c, d je teda lineárne nezávislý od toho їх kolkіst dorіvnyuє razmіrnostі vektorový priestor, tiež a, b, c, d є tý základ.
Návrh:
Vihіdnі vectori є základ chotirivimіrnogo rozloha.
zadok.
Chi sa stať vektorom a základom vektorovej rozlohy priestoru 4?
Riešenie.
Navіt ako vihіdna systém vektorov je lineárne nezávislý, počet vektorov v ňom nestačí na to, aby bol základom chotirivimirového priestoru (základ takéhoto priestoru je zložený zo 4 vektorov).
Návrh:
Nie, neskladajte.
Rozloženie vektora na báze vektorového priestoru.
Dajte mi nejaké vektory є základ vektorového priestoru n-sveta. Ak k nim pridáme n-virtuálny vektor x, tak systém vektorov bude lineárne ladený. Zo sily lineárneho úhoru vieme, že ak jeden vektor lineárneho úhorového systému je lineárne vyjadrený cez ostatné. Inými slovami, ak je jeden z vektorov v lineárnom úhorovom systéme umiestnený za inými vektormi.
Tak sme sa priblížili k dôležitej teórii.
Veta.
Či je vektor n-svetového vektorového priestoru distribuovaný v jednom poradí podľa základu.
Prinášanie.
Poď - Základ n-svetového vektorového priestoru. Dodamo to tsikh vector_v n-svetový vektor x. Potom bude sústava vektorov lineárne ladná a vektor x môže byť lineárne vyjadrený pomocou vektorov. : de - deakі čísla. Za základ sme teda zobrali rozloženie vektora x. Stratené priniesť, scho rozladannya edine.
Je prijateľné, že existuje ešte jedno rozloženie, de 
- Skutočné čísla. Je to vidieť z ľavej a pravej časti zostávajúcej rovnosti, je to zrejmé z ľavej a pravej časti rovnosti:
Oskilkiho systém bázových vektorov je lineárne nezávislá, potom z dôvodu označenia lineárnej nezávislosti sústavy vektorov je rovnosť možná len vtedy, ak sú všetky koeficienty rovné nule. Ten, kto prináša jednotu rozloženia vektora podľa základu.
Vymenovanie.
Koeficienty sa nazývajú súradnice vektora x v zákl .
Keďže poznáme vetu o šírení vektora podľa základu, začíname chápať podstatu „vektorových úloh n-sveta“ 
". Tse znamená, že uvažujeme vektor x n-svetového vektorového priestoru, súradnice ľubovoľnej danej úlohy v danej báze. Podľa nášho najlepšieho názoru, že vektor x v inom základe n-svetového vektorového priestoru bude mať súradnice, vіdminnі vіd .
Pozrime sa na túto úlohu.
Zoberme si systém n lineárne nezávislých vektorov pre danú bázu n-svetového vektorového priestoru 
ta vektor . Todi vektory є je tiež základom tohto vektorového priestoru.
Dajte nám vedieť súradnice vektora x v základe . Výrazne q súradnice jaka .
Vektor x y základ mohli byť nahlásené. Zapíšme si rovnosť súradnicového tvaru:
Tsya rіvnіst rіvnostrong systemі z n_linear rіvnіnі algebra z n nevіdomimi zminnimi :
Je možné vidieť hlavnú maticu systému 
Výrazne її písmeno A. Stovptsі matice A є vektory lineárne nezávislého systému vektorov. Preto sa hodnosť matice rovná n, tiež її vyznachnik vіdminny vіd nula. Táto skutočnosť poukazuje na tie, že sústava sa môže rovnať jednému riešeniu, ktoré možno nájsť akoukoľvek metódou, napr.
Tak zistíte súradnice vektor x y základ .
Poďme analyzovať teóriu z aplikácií.
zadok.
V skutočnom základe trivi- merového vektorového priestoru sú dané vektory 
Znova si uvedomte, že systém vektorov je tiež základom tohto priestoru a z tohto základu pozná súradnice vektora x.
Riešenie.
Aby systém vektorov bol základom triviálneho priestoru, bolo potrebné, aby bol lineárne nezávislý. Je jasné, že poradie matice A je určené riadkami vektorov. Poradie známe Gaussovou metódou 
Tiež Rank(A) = 3, čo ukazuje lineárnu nezávislosť vektorového systému.
Základom je opäť vektor. Nech má základný vektor x maє súradnice. Potom, ako sme si ukázali viac, prepojenie súradníc tohto vektora je dané vyrovnávacím systémom 
Podriaď sa jej, mysli na význam, ber ho preč 
Virishimo її Cramerova metóda: 
Takto vektor x v základe nemá žiadne súradnice 
.
Návrh:
zadok.
Na základe diacom 
vektorový priestor chotirivimir je daný lineárne nezávislým systémom vektorov 
Vіdomo scho 
. Nájdite súradnice vektora x v základe .
Riešenie.
Oskіlki vektorový systém 
lineárne nezávislý od mysle, je základom chotirivimirovej rozlohy. Todі rivnіst znamená, že vektor x je v zákl dokáže koordinovať. Výrazne súradnice vektora x v zákl jaka.
Systém zarovnania, ktorý nastavuje väzbu súradníc vektora x v bázach і môže zobraziť 
Nahraďte v ňom dané hodnoty a známe súradnice: 
Návrh:
.
Prepojenie medzi základňami.
Nech daný základ n-svetového vektorového priestoru nastaví dva lineárne nezávislé vektorové systémy 
і
Tobto, smrad je tiež základom tejto rozlohy.
Yakscho 
- súradnice vektora na zákl , potom odkaz súradníc 
і nastavený systémom lineárnych čiar (hovorili o nás v prvom bode): 
, v matričnom tvare sa môže písať ako 
Podobne pre vektor môžeme písať 
Rovnosti doprednej matice možno spojiť do jednej, ktorá v skutočnosti nastaví väzby vektorov na dve rôzne bázy. 
Podobne môžeme uviesť všetky vektory a základ cez základ 
:
Vymenovanie.
Matrix 
názov prechodová matica na základ na základ aj vtedy je rovnosť spravodlivá 
Po znásobení urážok sú časti ceny ekvivalencie pravotočivé
prijaté 
Poznáme prechodovú maticu, pod ktorou nebudeme referovať o známej pivotnej matici a násobených maticiach (čuduj sa potrebe štatistiky): 
Stratené vektorové súradnice z'yasuvati zv'yazok v daných základniach.
Nech má teda základný vektor x súradnice 
a základom je vektor x a súradnice , teda 
Zvyšné časti zostávajúcich dvoch rovníc sú rovnaké, môžeme prirovnať pravé časti: 
Ako znásobiť urážky pravorukých častí na
potom berieme 
Z druhej strany 
(Poznajte reverznú maticu sami).
Dve zostávajúce rovnosti nám poskytujú zoznam väzieb súradníc vektora x v základoch i .
Návrh:
Je možné zobraziť maticu prechodu od základu k základu 
;
súradnice vektora x v základoch a spojené s 
alebo .
Pozreli sme sa na pochopenie diverzity a základu vektorového priestoru, naučili sme sa rozložiť vektor podľa základu a ukázali sme prepojenie medzi rôznymi základňami n-svetového priestoru vektora cez prechodovú maticu.
Strana 1
Pіdprostir, jogo základ a rozmirnіst.
Poď L- Lineárny priestor nad poľom P і A- čiastkové s L. Yakscho A uložte riadkový priestor nad poľom P ako tiché sú samotné prevádzky, aké L, potom A nazývame podpriestor priestoru L.
Vіdpovіdno až do vymenovania lineárneho priestoru, shob A bolo potrebné pre priestor prehodnotiť existenciu A operácie:
1) : 
;
2) 
: 
;
a overte, či operácie v A zoradenie ôsmich axióm. Prote zostane zayvim (za to, že axiómy sú napísané v L) vám. férová ofenzíva
Veta. Nech L vedie priestor nad poľom P i 
. Neosobné A todі і menej tоdі є pіdprostorom L, ak takíto vimogi zvíťazia:
1. : ;
2. : .
Pevnosť. Yakscho L – n-pokojný lineárny priestor, ktorý A joga pіdprostіr, teda A tiež konečný lineárny priestor a jogová expanzia nepresahujú n.
P 
príklad 1. Chi є pіdprostorom priestor vectorіv-vіdrіzkіv V2 neosobné S všetky vektorіv oblasť, koža z yah leží na jednej z osí súradníc 0x alebo 0y?
Riešenie: Poď 
, 
і 
, 
. Todi 
. Otzhe, S nie je podpriestor 
.
zadok 2. V 2 vectorіv-vіdrіzkіv rovina bez lіch S všetky vektory v rovine, na klase a kіntsі tých ležia na tejto priamke l aká oblasť?
Riešenie.
E 
sli vektor 
vynásobiť číslom k, potom vezmeme vektor 
, tiež si ľahnúť S. Yakshcho 
і 
sú potom dva vektory z S 
(podľa pravidla skladania vektorov na priamku). Otzhe, S є pіdprostorom 
.
Príklad 3 Chi є lineárny podpriestor lineárneho priestoru V 2 bez tváre A všetkých vektorov v rovine l, (Predpokladajme, že klas akéhokoľvek vektora zbіgaєtsya s klasom súradníc)?
R 
Riešenie.
Občas, ak je rovný l neprechádzajte cez klas súradníc ALE lineárny podpriestor V 2
nie є, pretože 
.
Občas, ak je rovný l
prejsť klasom súradníc, bez tváre ALEє lineárny podpriestor V 2
,
pretože 
i pri multiplikátore ľubovoľného vektora 
číslo na ciferníku α
z poľa R prijaté 
. V tomto rangu je okrem lineárneho priestoru pre multiplicitu ALE vikonanі.
Príklad 4. Nech je daný systém vektorov 
z lineárneho priestoru L nad ihriskom P. Aby sme priniesli, že neexistujú rôzne lineárne kombinácie 
s koeficientmi 
h Pє podpriestor L(cez pіdprosіr A nazývaný podpriestor, generovaný systémom vektorov alebo lineárny plášť vektorové systémy, a označte takto: 
alebo 
).
Riešenie. Pravda, k tomu, potom na akékoľvek prvky X,
r
A možno: 
, 
, de 
, 
. Todi
tak jaka , potom 
k tomu 
.
Prehodnoťme platnosť ďalšej myšlienky vety. Yakscho X- byť vektorom Aі t- nech je to číslo z P, potom. Oskilki 
і 
,, potom 
, k tomu 
. V tomto poradí, zgіdno z vety, neosobné A- Rozloha lineárneho priestoru L.
Pre posledné lineárne priestory je to spravodlivé a reverzibilné.
Veta. Be-yaky pіdprostіr ALE lineárny priestor L nad ihriskom 
є lineárny obal spevového systému vektorov.
Keď razv'yazannі problém znakhodzhennya základ a razmіrnostі linіynoї okolonka vikoristovuyu prísť teorém.
Veta. Základ lineárneho plášťa 
pracovať so základom vektorového systému . Rozšírenie lineárneho puzdra kolíše s hodnosťou vektorového systému .
Príklad 4. Poznať základ a rozšírenie priestoru 
lineárny priestor R 3
[
X]
, Páči sa mi to 
, 
, 
, 
.
Riešenie. Vіdomo, scho vektory a їх súradnicové riadky (stovptsі) môžu mať rovnakú silu (zobraziť lineárny úhor). Pridanie matice A=
zo súradnicových vektorov 
na základni 
.
Poznáme hodnosť matice A.
. M 3
=
. 
.
Otec, hodnosť r(A)=
3. Tiež hodnosť systému vektorov viac 3. Neskôr je expanzia podpriestoru S viac 3, keďže základ je zložený z troch vektorov 
(pretože v základnej moll 
zadajte súradnice týchto vektorov)., . Vektorový systém Tsya je lineárne nezávislý. Dobre, no tak.
І 
.
Môžete prehodnotiť, aký systém 
lineárne úhor pre akýkoľvek vektor X h H. Cim priniesol sho 
maximálny lineárne nezávislý systém vektorov v podpriestore H, potom. - základ y H ta dim H=n 2
.
strana 1
Lineárny priestor V sa nazýva n-mier ako v novom systéme, systém n lineárne nezávislých vektorov a či je systém s väčším počtom vektorov lineárne nezávislý. Volá sa číslo n rozmirnistyu (počet vimiriv) lineárny priestor V i je označený \operatorname(dim)V. Inými slovami, expanzia priestoru je maximálny počet lineárne nezávislých vektorov v tomto priestore. Ako taký kіlkіst іsnuє, potom sa rozloha nazýva kіtsev. Ak má priestor V pre akékoľvek prirodzené číslo n systém, ktorý sa skladá z n lineárne nezávislých vektorov, potom sa takýto priestor nazýva nevyčerpateľný (zapíšte si: \operatorname(dim)V=\infty). Ďaleko, akoby nie múdro nepriateľské, budú hľadieť na rozlohy konca.
Základ Lineárna rozloha n-sveta sa nazýva usporiadaná kolekcia n lineárne nezávislých vektorov ( bázové vektory).
Veta 8.1 o expanzii vektora za bázou. Ak je základom n-svetového lineárneho priestoru V , potom každý vektor \mathbf(v)\in V môže mať reprezentácie v lineárnej kombinácii základných vektorov:
\mathbf(v)=\mathbf(v)_1\cdot \mathbf(e)_1+\mathbf(v)_2\cdot \mathbf(e)_2+\ldots+\mathbf(v)_n\cdot \mathbf(e)_n
a pred tou istou hodnosťou tobto. koeficient \mathbf(v)_1, \mathbf(v)_2,\ldots, \mathbf(v)_n jasne vyniknúť. Inými slovami, či už je v priestore vektor, môžu existovať usporiadania podľa základu a až do rovnakej hodnosti.
Pravda, otvorenosť priestoru V dorіvnyuє n. Vektorový systém \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n lineárne nezávislé (ce základ). Keď sa dostaneme k základu ľubovoľného vektora \mathbf(v), môžeme použiť lineárne ležiaci systém \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n, \mathbf(v)(Mierky tohto systému sú zložené z (n + 1) vektorov v n-svetovom priestore). Kvôli 7 lineárne ležiacim a lineárne nezávislým vektorom môžeme vziať počet viet.
Posledná 1. Yakscho \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n je základom pre priestor V , teda V=\názov operátora(Lin) (\mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_n), potom. Lineárna rozloha je lineárna obálka základných vektorov.
Pravda, dokázať rovnocennosť V=\názov operátora(Lin) (\mathbf(e)_1,\mathbf(e)_2, \ldots, \mathbf(e)_n) dva tucty dosit ukážte, že ste súčasťou V\subset \operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_n) a prihlásia sa naraz. V skutočnosti z jednej strany, či už ide o lineárnu kombináciu vektorov v lineárnom priestore, ktoré ležia na samotnom lineárnom priestore, tj. \operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n)\podmnožina V. Na druhej strane, či je akýkoľvek vektorový priestor nad vetou 8.1 možný ako lineárna kombinácia základných vektorov. V\subset \operatorname(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n). Môžete vidieť vyrovnanosť pohľadu na zástupy.
Posledné 2. Yakscho \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- lineárne nezávislý systém vektorov v lineárnom priestore V a či vektor \mathbf(v)\in V môže mať zobrazenia v lineárnej kombinácii (8.4): \mathbf(v)=v_1\mathbf(e)_1+ v_2\mathbf(e)_2+\ldots+v_n\mathbf(e)_n, potom priestor V môže expandovať n a systém \mathbf(e)_1,\mathbf(e)_2, \ldots,\mathbf(e)_nє základ jogy.
V skutočnosti má priestor V systém n lineárne nezávislých vektorov, ale bez ohľadu na to, či ide o systém \mathbf(u)_1,\mathbf(u)_2,\ldots,\mathbf(u)_n pri väčšom počte vektorov (k>n) je lineárne ladený, črepy kožných vektorov zo systému sú lineárne vyjadrené cez vektory \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n. Znamenať, \operatorname(dim) V=nі \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- Základ V.
Veta 8.2 ako rozšíriť systém vektorov na bázu. Buď lineárne nezávislý systém k vektorov v n-svetovom lineárnom priestore (1\leqslant k Pravda, nech je to - lineárne nezávislý systém vektorov v priestore n-sveta V~(1\leqslant k Rešpekt 8.4 1. Základ lineárneho priestoru je nejednoznačný. Napríklad ako \mathbf(e)_1,\mathbf(e)_2, \ldots, \mathbf(e)_n je základ pre priestor V , potom systém vektorov \lambda \mathbf(e)_1,\lambda \mathbf(e)_2,\ldots,\lambda \mathbf(e)_n lebo čokoľvek \lambda\ne0 je aj základom V . Počet základných vektorov v rôznych bázach jedného a toho istého konečne-dimenzionálneho priestoru je, samozrejme, rovnaký, sú to rovnaké oscilácie rovnakého počtu bohatosti priestoru. 2. V niektorých otvorených priestoroch, ktoré sa často používajú v prístavbách, sa jeden z možných podkladov, z praktického hľadiska najpraktickejší, nazýva štandardný. 3. Veta 8.1 nám umožňuje povedať, že báza je reálny systém prvkov v lineárnom priestore, teda ktorýkoľvek vektorový priestor je lineárne vyjadrený prostredníctvom vektorov báz. 4. Yakscho neosobné \mathbb(L) є lineárna škrupina \operatorname(Lin)(\mathbf(v)_1,\mathbf(v)_2,\ldots,\mathbf(v)_k), potom vektory \mathbf(v)_1,\mathbf(v)_2,\ldots,\mathbf(v)_k nazývané uspokojujúce multiplikátory \mathbb(L) . Posledný 1 z vety 8.1 prostredníctvom rovnosti V=\meno operátora(Lin) (\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n) dovoľte mi povedať, že základ je minimálny systém utvoryuyuchih lineárny priestor V , takže nie je možné zmeniť počet vyhovujúcich (ak chcete vidieť jeden vektor z množiny \mathbf(e)_1, \mathbf(e)_2,\ldots,\mathbf(e)_n) bez ujmy na vlastnom imaní V=\meno operátora(Lin)(\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n). 5. Veta 8.2 nám umožňuje povedať, že základ je maximálny lineárne nezávislý systém vektorov lineárna rozloha, črepy základu - úplne lineárne nezávislý systém vektorov a nie je možné ho doplniť vektorom bez straty lineárnej nezávislosti. 6. Najnovšia 2 vety 8.1 na manuálne fixovanie významu základne a rozmernosti lineárneho priestoru. Nie je správne, aby niektorí asistenti prijali na základe menovania, ale pre seba: lineárny nezávislý systém \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n vektor v lineárnom priestore sa nazýva báza, ako keby sa vektor v priestore lineárne otáčal cez vektory \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n. Počet základných vektorov určuje rozmanitosť priestoru. Bude zrejmé, že označenie je ekvivalentné s ukazovaním vyššie. Napríklad rozmіrnіst i základ pre buttіv іnіynykh rozlohy, razglyuṇuh vysche. 1. Nulový lineárny priestor \(\mathbf(o)\) nepomstí lineárne nezávislé vektory. Preto sa rozmіrnіst tejto rozlohy vvazhut rovná nule: \dim\(\mathbf(o)\)=0. Tsei prostіr žiadny základ. 2. Medzery V_1,\,V_2,\,V_3 možno oddeliť 1, 2, 3 bežným spôsobom. To, či akýkoľvek nenulový vektor k priestoru V_1 vytvára lineárne nezávislý systém (oddelenie 1. podľa 8.2), a či sú dva nenulové vektory k priestoru V_1 kolineárne, tzn. lineárne usadeniny (div. zadok 8.1). Tiež \dim(V_1)=1 a základom priestoru V_1 je vektor. Podobne sa dá tvrdiť, že \dim(V_2)=2 a \dim(V_3)=3 . Základom priestoru V_2 môžu byť dva nekolineárne vektory v rovnakom poradí (jeden z nich je považovaný za prvý základný vektor, druhý - druhý). Základom priestoru V_3 sú tri nekoplanárne (ktoré neležia v rovnakých alebo rovnobežných rovinách) vektory zobraté v rovnakom poradí. Štandardný základ V_1 je jeden vektor \ vec (i) na riadku. Štandardný základ pre V_2 je základ \vec(i),\,\vec(j), ktorý je vytvorený z dvoch navzájom kolmých jednoduchých vektorov v rovine. Štandardným základom pre priestor V_3 je základ \vec(i),\,\vec(j),\,\vec(k), Skladby troch jednoduchých párových kolmých vektorov, ktoré spĺňajú správnu trojicu 3. Priestor \mathbb(R)^n na pomstu nie viac ako n lineárne nezávislých vektorov. V skutočnosti zoberieme k stĺpcov \mathbb(R)^n a zložíme ich do expanznej matice n\krát k . Ak k>n, potom sú hodnoty lineárne závislé od vety 3.4 o poradí matice. Otzhe, \dim(\mathbb(R)^n)\leqslant n. V priestore \mathbb(R)^n nie je dôležité poznať lineárne nezávislé stĺpce. Napríklad stĺpce jednej matice \mathbf(e)_1=\začiatok (pmatrix)1\\0\\\vdots\\0\koniec (pmatrix)\!,\quad \mathbf(e)_2= \začiatok (pmatrix)0\\1\ \\vdots\\0\end(pmatrix)\!,\quad \ldots,\quad \mathbf(e)_n= \begin(pmatrix) 0\\0\\vdots\\1 \end(pmatrix)\ ! . lineárne nezávislé. Otzhe, \dim(\mathbb(R)^n)=n. Zavolá sa priestor \mathbb(R)^n n-svetový rečový aritmetický priestor. Množinu vektorov berie do úvahy štandardná báza priestoru \mathbb(R)^n. Podobne možno tvrdiť, že \dim(\mathbb(C)^n)=n k tomu sa volá \mathbb(C)^n n-svetový komplexný aritmetický priestor. 4. Tipovať, že ak sa dá na pohľad zdaniť riešenie homogénnej sústavy Ax=o x=C_1\varphi_1+C_2\varphi_2+\ldots+C_(n-r)\varphi_(n-r), de r=\meno operátora(rg)A, a \varphi_1,\varphi_2,\ldots,\varphi_(n-r)- základný systém riešení. Otzhe, \(Ax=o\)=\názov operátora(Lin) (\varphi_1,\varphi_2,\ldots,\varphi_(n-r)), potom. základom priestorového \(Ax=0\) riešenia homogénneho systému je fundamentálne systémové riešenie a veľkosť priestoru \dim\(Ax=o\)=n-r de n je počet nehomogénnych a r je poradie matice systému. 5. V priestore M_(2\times3) matica expanzie 2\times3 môžete vybrať 6 matíc: \začiatok(zhromaždené)\mathbf(e)_1= \začiatok(pmatrix)1&0&0\\0&0&0\koniec(pmatrix)\!,\quad \mathbf(e)_2= \začiatok(pmatrix)0&1&0\\0&0&0\end( pmatrix)\!,\quad \mathbf(e)_3= \begin(pmatrix) 0&0&1\\0&0&0\end(pmatrix)\!,\hfill\\ \mathbf(e)_4= \begin(pmatrix) 0&0&0\\ 1&0&0 \end(pmatrix)\!,\quad \mathbf(e)_5= \začiatok (pmatrix)0&0&0\\0&1&0\end(pmatrix)\!,\quad \mathbf(e)_6= \begin(pmatrix)0&0&0 \\0&0&1\end(pmatrix)\!,\hfill \end(zhromaždené) \alpha_1\cdot \mathbf(e)_1+\alpha_2\cdot \mathbf(e)_2+\alpha_3\cdot \mathbf(e)_3+ \alpha_4\cdot \mathbf(e)_4+\alpha_5\cdot \\cdot\alpha_6 \mathbf(e)_6= \begin(pmatrix)\alpha_1&\alpha_2&\alpha_3\\ \alpha_4&\alpha_5&\alpha_6\end(pmatrix) lepšia nulová matica je menej pre triviálnu \alpha_1=\alpha_2= \ldots= \alpha_6=0. Po prečítaní rovnosti (8.5) z pravej strany sa stanovuje, že matica skinu s M_(2\times3) v lineárnom poradí je vyjadrená prostredníctvom vybraných 6 matíc, tj. M_(2\times)= \operatorname(Lin) (\mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_6). Otzhe, \dim(M_(2\times3))=2\cdot3=6 a matrice \mathbf(e)_1, \mathbf(e)_2,\ldots,\mathbf(e)_6є základ (štandard) tohto priestoru. Podobne možno tvrdiť, že \dim(M_(m\krát n))=m\cdot n. 6. Pre ľubovoľné prirodzené n v priestore P(\mathbb(C)) bohaté členy s komplexnými koeficientmi možno poznať lineárne nezávislé prvky. Napríklad bohaté výrazy \mathbf(e)_1=1, \mathbf(e)_2=z, \mathbf(e)_3=z^2,\,\ldots, \mathbf(e)_n=z^(n-1) lineárne nezávislé, črepy línie a_1\cdot \mathbf(e)_1+a_2\cdot \mathbf(e)_2+\ldots+a_n\cdot \mathbf(e)_n= a_1+a_2z+\ldots+a_nz^(n-1) viac podobný nulovému bohatému členu (o(z)\equiv0) menej ako triviálnemu a_1=a_2=\ldots=a_n=0. Oskіlki tsya systém bohato definovaných pojmov je lineárne nezávislý od akéhokoľvek prirodzeného l, priestor P(\mathbb(C)) nie je obmedzený. Podobným spôsobom pracujeme o nevyčerpateľnom rozširovaní priestoru P(\mathbb(R)) s bohatými členmi s efektívnymi koeficientmi. Rozšírenie P_n(\mathbb(R)) už nemá bohatšie segmentované kroky, nižších n koncov. Naozaj, vektory \mathbf(e)_1=1, \mathbf(e)_2=x, \mathbf(e)_3=x^2,\,\ldots, \mathbf(e)_(n+1)=x^n spĺňajú (štandardný) základ tohto priestoru, takže smrady sú lineárne nezávislé a akýkoľvek polynóm v P_n(\mathbb(R)) môže byť reprezentovaný vo vizuálne lineárnej kombinácii týchto vektorov: a_nx^n+\ldots+a_1x+a_0=a_0\cdot \mathbf(e)_1+a_1 \mathbf(e)_2+\ldots+a_n\cdot \mathbf(e)_(n+1)Použiť základy lineárnych priestorov
yakі lineárne nezávislé. Je pravda, že ide o lineárnu kombináciu
7. Rozsah C(\mathbb(R)) neprerušiteľných funkcií je nekonečne pokojný. Pravda, pre každého prírodného n bohatého 1,x,x^2,\ldots, x^(n-1), Sú vnímané ako neprerušované funkcie, ktoré vytvárajú lineárne nezávislé systémy (úžasný predný zadok).
Vo vesmíre T_(\omega)(\mathbb(R)) trigonometrické binomy (frekvencie \omega\ne0 ) s efektívnymi koeficientmi, základ vyhovuje monomizmom \mathbf(e)_1(t)=\sin\omega t,~\mathbf(e)_2(t)=\cos\omega t. Smrad je lineárne nezávislý, črepiny sú samá žiarlivosť a\sin\omega t+b\cos\omega t\equiv0 možno menej pre triviálnu náladu (a=b=0) . Nech je to funkcia mysle f(t)=a\sin\omega t+b\cos\omega t lineárne vyjadrené prostredníctvom základov: f(t)=a\,\mathbf(e)_1(t)+b\,\mathbf(e)_2(t).
8. Rozšírenie \mathbb(R)^X aktuálnych funkcií, priradených k násobkom X, v oblasti priradenia X môže byť konečné alebo nevyčerpateľné. Ak X je kіntsevy multiplikátor, potom priestor \mathbb(R)^X je kіntsev (napr. X=\(1,2,\ldots,n\)). Ak je X neosobné, potom priestor \mathbb(R)^X nie je obmedzený (napríklad priestor \mathbb(R)^N sekvencií).
9. V priestore \mathbb(R)^(+), či je číslo \mathbf(e)_1 kladné, nie rovné jednej, môže byť základom. Vezmime si napríklad číslo \mathbf(e)_1=2. Či je číslo r nejakým spôsobom kladné, sa dá povedať pomocou \mathbf(e)_1 . ukázať na pohľad \alpha\cdot \mathbf(e)_1\colon r=2^(\log_2r)=\log_2r\ast2=\alpha_1\ast \mathbf(e)_1, de \alpha_1=\log_2r. Tiež rozšírenie, ktorého priestor sa rovná 1, je základom číslo \mathbf(e)_1=2.
10. Poď \mathbf(e)_1,\mathbf(e)_2,\ldots,\mathbf(e)_n- Základ rečového lineárneho priestoru V. Významne na V lineárnej skalárnej funkcii, pomocou:
\mathcal(E)_i(\mathbf(e)_j)=\začiatok(prípady)1,&i=j,\\ 0,&i\ne j.\koniec(prípady)
V tomto prípade je kvôli linearite funkcie \mathcal(E)_i pre určitý vektor potrebné \mathcal(E)(\mathbf(v))=\sum_(j=1)^(n)v_j \mathcal(E)(\mathbf(e)_j)=v_i.
Neskôr bolo priradených n prvkov (kovektorov). \mathcal(E)_1, \mathcal(E)_2, \ldots, \mathcal(E)_n získané do priestoru V^(\ast) . Dajte nám to vedieť \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_n- Základ V^(\ast).
Najprv si ukážme, že systém \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_n lineárne nezávislé. Pravda, zoberte lineárnu kombináciu týchto vektorov (\alpha_1 \mathcal(E)_1+\ldots+\alpha_n\mathcal(E)_n)(\mathbf(v))= to sa rovná nulovej funkcii
\mathbf(o)(\mathbf(v))~~ (\mathbf(o)(\mathbf(v))=0~ \forall \mathbf(v)\in V)\colon~ \alpha_1\mathcal(E )_1(\mathbf(v))+\ldots+\alpha_n\mathcal(E)_n(\mathbf(v))= \mathbf(o)(\mathbf(v))=0~~\forall \mathbf(v )\vo V.
Podriaďovanie sa qiu vyrovnanosti \mathbf(v)=\mathbf(e)_i,~ i=1,\ldots,n, berieme \alpha_1=\alpha_2\cdot= \alpha_n=0. Otze, sústava prvkov \mathcal(E)_1,\mathcal(E)_2,\ldots,\mathcal(E)_n priestor V^(\ast) je od toho lineárne nezávislý \alpha_1\mathcal(E)_1+\ldots+ \alpha_n\mathcal(E)_n =\mathbf(o) možno menej pre triviálny pohľad.
Iným spôsobom možno ukázať, že lineárnu funkciu f\in V^(\ast) možno vidieť z lineárnej kombinácie kovektorov \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_n. Deisno, pre akýkoľvek vektor \mathbf(v)=v_1 \mathbf(e)_1+v_2 \mathbf(e)_2+\ldots+v_n \mathbf(e)_n cez linearitu funkcie f môžeme vziať:
\begin(aligned)f(\mathbf(v))&= f(v_1 \mathbf(e)_1+\ldots+v_n \mathbf(e)_n)= v_1 f(\mathbf(e)_1)+\ldots+ v_n f(\mathbf(e)_n)= f(\mathbf(e)_1)\mathcal(E)_1(\mathbf(v))+ \ldots+ f(\mathbf(e)_n)\mathcal(E) _n (\mathbf(v))=\\ &=(f(\mathbf(e)_1)\mathcal(E)_1+\ldots+ f(\mathbf(e)_n)\mathcal(E)_n)(\mathbf ( v))= (\beta_1\mathcal(E)_1+ \ldots+\beta_n\mathcal(E)_n) (\mathbf(v)),\end(zarovnané)
tobto. funkcia f je reprezentovaná ako lineárna kombinácia f=\beta_1 \mathcal(E)_1+\ldots+\beta_n\mathcal(E)_n funkcie \mathcal(E)_1,\mathcal(E)_2,\ldots, \mathcal(E)_n(čísla \beta_i=f(\mathbf(e)_i)- Lineárne kombinačné koeficienty). Otze, systém covektorov \mathcal(E)_1, \mathcal(E)_2,\ldots, \mathcal(E)_nє základ výsledného priestoru V^(\ast) i \dim(V^(\ast))=\dim(V)(Pre posledné miesto V).
Ako si pripomenúť omilostenie, omilostenie kamaráta či propozície, napíšte do komentárov.
Sústavy lineárnych rovnomerných čiar
Nastavenie problému. Poznať základ a znamenať rozšírenie lineárneho priestoru riešenia sústavy
Plán rozvyazannya.
1. Napíšte maticu systému:
A pomocou elementárnych transformácií môžeme matricu prerobiť do trikotovej podoby, tobto. k takémuto pohľadu, ak sa všetky prvky, ktoré sa nachádzajú pod uhlopriečkou hlavy, rovnajú nule. Poradie matice systému sa rovná počtu lineárne nezávislých riadkov, teda v našom prípade počtu riadkov, v ktorých chýbajú nenulové prvky:
Riešením je otvorenosť priestoru. Ak áno, potom homogénny systém môže mať jediné nulové riešenie, ak áno, potom systém môže mať neosobné riešenie.
2. Vyberáme základné a voľné. Významný je Vilni zminnі. Potom zmeníme základné zmeny cez jazdné pruhy, otrimavshi v takom poradí konečné riešenie jednotného systému lineárnych zarovnaní.
3. Základ pre priestor riešenia sústavy zapíšeme za sebou jednu z najväčších meniteľných rovnakých jednotiek, inak nulu. Rozšírenie lineárneho priestoru je riešením systému na zvýšenie počtu vektorov v základe.
Poznámka. Pred elementárnymi transformáciami matice je možné pridať:
1. násobenie (rozpodіl) riadku násobiteľom, vіdminny vіd nula;
2. pridanie do ďalšieho riadku nasledujúceho riadku, vynásobené číslom;
3. permutácia radov subdecúd;
4. Prepracovanie 1-3 pre stovptsіv (v časoch rozvyazannya systémov lineárnych zarovnaní, elementárne prepracovanie stovptsіv nie je vicorated).
Úloha 3. Poznať základ a určiť expanziu lineárneho priestoru riešenia sústavy.
Zapíšeme si maticu systému a pomocou elementárnych transformácií ju privedieme do trojzubca:
Vážení teda
- V kontakte s 0
- Google+ 0
- OK 0
- Facebook 0
