Перед тим, як дати поняття векторного твору, звернемося до питання орієнтації впорядкованої трійки векторів a → , b → , c → у тривимірному просторі.

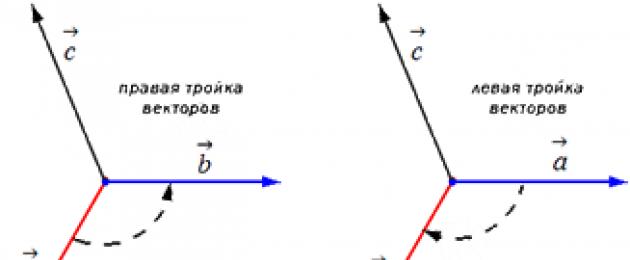
Відкладемо спочатку вектори a → , b → , c → від однієї точки. Орієнтація трійки a → , b → , c → буває правою чи лівою, залежно від напрямку самого вектора c → . Від того, в яку сторону здійснюється найкоротший поворот від вектора a → до b → з кінця вектора c → буде визначено вид трійки a → , b → , c → .

Якщо найкоротший поворот здійснюється проти годинникової стрілки, то трійка векторів a → , b → , c → називається правою, якщо за годинниковою стрілкою – лівий.

Далі візьмемо два не колінеарні вектори a → і b → . Відкладемо потім від точки A вектори AB → = a → і A C → = b → . Побудуємо вектор A D → = c → , який перпендикулярний одночасно і A B → і A C → . Таким чином, при побудові самого вектора A D → = c → ми можемо надійти подвійно, задавши йому або один напрямок, або протилежний (дивіться ілюстрацію).

Впорядкована трійка векторів a → , b → , c → може бути, як ми з'ясували правою чи лівою залежно від напрямку вектора.

Зі сказаного вище можемо ввести визначення векторного твору. Це визначення дається для двох векторів, визначених у прямокутній системі координат тривимірного простору.

Визначення 1

Векторним твором двох векторів a → та b → називатимемо такий вектор заданий у прямокутній системі координат тривимірного простору такий, що:

• якщо вектори a → та b → колінеарні, він буде нульовим;
• він буде перпендикулярний і вектору a → та вектору b → тобто. ∠ a → c → ∠ b → c → = π 2 ;
• його довжина визначається за формулою: c → = a → · b → · sin ∠ a → , b →;
• трійка векторів a → , b → , c → має таку саму орієнтацію, як і задана система координат.

Векторний добуток векторів a → та b → має таке позначення: a → × b → .

Координати векторного твору

Оскільки будь-який вектор має певні координати в системі координат, можна ввести друге визначення векторного твору, яке дозволить знаходити його координати за заданими координатами векторів.

Визначення 2

У прямокутній системі координат тривимірного простору векторним твором двох векторів a → = (a x ; a y ; a z) і b → = (b x ; b y ; b z) називають вектор c → = a → × b → = (ay · bz - az · by) · i → + (az · bx - ax · bz) · j → + (ax · by - ay · bx) · k → , де i → j → k → є координатними векторами.

Векторний твір можна представити як визначник квадратної матриці третього порядку, де перший рядок є вектори орти i → , j → , k → , другий рядок містить координати вектора a → , а третій – координати вектора b → у заданій прямокутній системі координат, даний визначник матриці виглядає так: c → = a → × b → = i → j → k → axayazbxbybz

Розклавши даний визначник за елементами першого рядка, отримаємо рівність: j → k → axayazbxbybz = ayazbybz · i → - axazbxbz · j → + axaybxby · k → = = a → × b → = (ay · bz - az · by) · i → + (az · bx - ax · bz) · j → + (ax · by - ay · bx) · k →

Властивості векторного твору

Відомо, що векторний твір в координатах представляється як визначник матриці c → = a → × b → = i → властивостей визначника матрицівиводяться такі властивості векторного твору:

1. антикомутативність a → × b → = - b → × a →;
2. дистрибутивність a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → або a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. асоціативність λ · a → × b → = λ · a → × b → або a → × (λ · b →) = λ · a → × b → , де λ - довільне дійсне число.

Ці властивості мають не складні докази.

Наприклад, можемо довести властивість антикомутативності векторного твору.

Доказ антикомутативності

За визначенням a → x b → = i → j → k → a x a y z b x b y b z і b → x a → = i → j → k → b x b y b z a x a y a z . А якщо два рядки матриці переставити місцями, то значення визначника матриці має змінюватися на протилежне, отже, a → x b → = i → j → k → axayazbxbybz = - i → j → k → bxbybzaxayaz = - b → × a → та доводить антикомутативність векторного твору.

Векторний твір – приклади та рішення

Найчастіше зустрічаються три типи завдань.

У задачах першого типу зазвичай задані довжини двох векторів та кут між ними, а потрібно знайти довжину векторного твору. У цьому випадку користуються наступною формулою c → a → b → sin ∠ a → , b → .

Приклад 1

Знайдіть довжину векторного добутку векторів a → та b → , якщо відомо a → = 3 , b → = 5 , ∠ a → , b → = π 4 .

Рішення

За допомогою визначення довжини векторного твору векторів a → та b → розв'яжемо дану задачу: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

Відповідь: 15 2 2 .

Завдання другого типу мають зв'язок із координатами векторів, у яких векторний твір, його довжина тощо. шукаються через відомі координати заданих векторів a → = (a x ; a y ; a z) і b → = (b x ; b y ; b z) .

Для такого типу завдань можна вирішити масу варіантів завдань. Наприклад, можуть бути задані не координати векторів a → і b → , які розкладання по координатним векторам виду b → = b x · i → + b y · j → + b z · k → і c → = a → × b → = (ay · bz - az · by) · i → + (az · bx - ax · bz) · j → вектори a → та b → можуть бути задані координатами точок їх початку та кінця.

Розглянемо такі приклади.

Приклад 2

У прямокутній системі координат задані два вектори a → = (2; 1; - 3), b → = (0; - 1; 1). Знайдіть їхній векторний твір.

Рішення

За другим визначенням знайдемо векторний добуток двох векторів у заданих координатах: a → × b → = (ay · bz - az · by) · i → + (az · bx - ax · bz) · j → + (ax · by - ay · bx) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2 · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .

Якщо записати векторний твір через визначник матриці, то рішення даного прикладу виглядає наступним чином: a → x b → = i → j → k → axayazbxbybz = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Відповідь: a → × b → = - 2 i → - 2 j → - 2 k → .

Приклад 3

Знайдіть довжину векторного добутку векторів i → - j → та i → + j → + k → , де i → , j → , k → - орти прямокутної декартової системи координат.

Рішення

Для початку знайдемо координати заданого векторного твору i → - j → × i → + j → + k → у цій прямокутній системі координат.

Відомо, що вектори i → - j → і i → + j → + k → мають координати (1; - 1; 0) і (1; 1; 1) відповідно. Знайдемо довжину векторного твору за допомогою визначника матриці, тоді маємо i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Отже, векторний твір i → - j → × i → + j → + k → має координати (-1; - 1; 2) у заданій системі координат.

Довжину векторного твору знайдемо за формулою (див. розділ довжини вектора): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

Відповідь: i → - j → × i → + j → + k → = 6 . .

Приклад 4

У прямокутній декартовій системі координат задані координати трьох точок A (1, 0, 1), B (0, 2, 3), C (1, 4, 2). Знайдіть якийсь вектор, перпендикулярний A B → і A C → одночасно.

Рішення

Вектори A B → і A C → мають наступні координати (- 1 ; 2 ; 2) та (0 ; 4 ; 1) відповідно. Знайшовши векторний добуток векторів A B → і A C → , очевидно, що він є перпендикулярним вектором за визначенням і до A B → , і до A C → , тобто є рішенням нашої задачі. Знайдемо його A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Відповідь: - 6 i → + j → - 4 k → . - один із перпендикулярних векторів.

Завдання третього типу орієнтовані використання властивостей векторного твору векторів. Після застосування яких будемо отримувати рішення заданого завдання.

Приклад 5

Вектори a → та b → перпендикулярні та їх довжини рівні відповідно 3 та 4 . Знайдіть довжину векторного твору 3 · a → - b → × a → - 2 · b → = 3 · a → × a → - 2 · b → + - b → × a → - 2 · b → = = 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .

Рішення

За властивістю дистрибутивності векторного твору ми можемо записати 3 · a → - b → × a → - 2 · b → = 3 · a → × a → - 2 · b → + - b → × a → - 2 · b → = = 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b →

За якістю асоціативності винесемо числові коефіцієнти за знак векторних творів в останньому виразі: 3 · a → × a → 3 · a → = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b →

Векторні твори a → × a → і b → × b → рівні 0, оскільки a → × a → = a → · a → · sin 0 = 0 і b → × b → = b → · b → 0 , тоді 3 · a → × a → - 6 · a → × b → - b → ? .

З антикомутативності векторного твору випливає - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × b → . .

Скориставшись властивостями векторного твору, отримуємо рівність 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

За умовами вектори a → та b → перпендикулярні, тобто кут між ними дорівнює π 2 . Тепер залишається лише підставити знайдені значення у відповідні формули: 3 · a → - b → ? → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .

Відповідь: 3 · a → - b → × a → - 2 · b → = 60 .

Довжина векторного твору векторів за орпеділенням дорівнює a → × b → = a → · b → · sin ∠ a → , b → . Оскільки вже відомо (зі шкільного курсу), площа трикутника дорівнює половині добутку довжин двох сторін помножене на синус кута між цими сторонами. Отже, довжина векторного добутку дорівнює площі паралелограма - подвоєного трикутника, а саме добутку сторін у вигляді векторів a → і b → відкладені від однієї точки на синус кута між ними sin ∠ a → , b → .

Це і є геометричний сенс векторного твору.

Фізичний сенс векторного твору

У механіці, одному з розділів фізики завдяки векторному твору можна визначити момент сили щодо точки простору.

Визначення 3

Під моментом сили F → ​​, прикладеної до точки B , щодо точки A розумітимемо наступний векторний твір A B → × F → .

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter

На цьому уроці ми розглянемо ще дві операції з векторами: векторний добуток векторіві змішаний твір векторів (відразу посилання, кому потрібне саме воно). Нічого страшного, так іноді буває, що для повного щастя, крім скалярного твору векторів, Потрібно ще і ще. Така ось векторна наркоманія. Може скластися враження, що ми залазимо в нетрі аналітичної геометрії. Це не так. У цьому розділі вищої математики взагалі мало дров, хіба що на Буратіно вистачить. Насправді матеріал дуже поширений і простий – навряд чи складніше, ніж те саме скалярний твір, навіть типових завдань буде менше. Головне в аналітичній геометрії, як багато хто переконається чи вже переконався, НЕ ПОМИЛИТИСЯ У ВИЧИСЛЕННЯХ. Повторюйте як заклинання, і буде вам щастя.

Якщо вектори виблискують десь далеко, як блискавки на горизонті, не біда, почніть з уроку Вектори для чайників, щоб відновити або знов придбати базові знання про вектори. Більш підготовлені читачі можуть ознайомлюватися з інформацією вибірково, я постарався зібрати максимально повну колекцію прикладів, які часто зустрічаються у практичних роботах

Чим вас одразу порадувати? Коли я був маленьким, то умів жонглювати двома і навіть трьома кульками. Спритно виходило. Зараз жонглювати не доведеться взагалі, оскільки ми розглядатимемо тільки просторові вектори, а плоскі вектори із двома координатами залишаться за бортом. Чому? Такими вже народилися дані дії – векторне та змішане твір векторів визначено та працюють у тривимірному просторі. Вже простіше!

У цій операції, так само, як і в скалярному творі, беруть участь два вектори. Нехай це будуть нетлінні літери.

Сама дія позначаєтьсянаступним чином: . Існують і інші варіанти, але я звик позначати векторний твір векторів саме так, у квадратних дужках із хрестиком.

І відразу питання: якщо в скалярному творі векторівберуть участь два вектори, і тут теж множаться два вектори, тоді в чому різниця? Явна різниця, перш за все, в РЕЗУЛЬТАТІ:

Результатом скалярного твору векторів є:

Результатом векторного твору векторів є ВЕКТОР: , тобто множимо вектори і знову отримуємо вектор. Закритий клуб. Власне, звідси й назва операції. У різній навчальної літературипозначення теж можуть варіюватися, я використовуватиму букву .

Визначення векторного твору

Спочатку буде визначення з картинкою, потім коментарі.

Визначення: Векторним твором неколлінеарнихвекторів, взятих у даному порядку, називається ВЕКТОР , довжинаякого чисельно дорівнює площі паралелограма, побудованого на даних векторах; вектор ортогональний векторам, і спрямований так, що базис має праву орієнтацію:

Розбираємо визначення по кісточках, тут багато цікавого!

Отже, можна назвати такі істотні моменти:

1) Вихідні вектори, позначені червоними стрілками, за визначенням не колінеарні. Випадок колінеарних векторів доречно буде розглянути трохи пізніше.

2) Вектори взяті у строго визначеному порядку: – "а" множиться на "бе", а чи не «бе» на «а». Результатом множення векторівє Вектор, який позначений синім кольором. Якщо вектори помножити у зворотному порядку, то отримаємо рівний за довжиною та протилежний у напрямку вектор (малиновий колір). Тобто справедливо рівність .

3) Тепер познайомимося із геометричним змістом векторного твору. Це надзвичайно важливий пункт! ДОВжина синього вектора (а, отже, і малинового вектора) чисельно дорівнює ПЛОЩІ паралелограма, побудованого на векторах. На малюнку цей паралелограм заштрихований чорним кольором.

Примітка : креслення є схематичним, і, природно, номінальна довжина векторного твору не дорівнює площі паралелограма.

Згадуємо одну з геометричних формул: площа паралелограма дорівнює добутку суміжних сторін на синус кута між ними. Тому, виходячи з вищесказаного, справедлива формула обчислення ДОВЖИНИ Векторного твору:

Підкреслюю, що у формулі йдеться про ДОВЖИНУ вектора, а не про сам вектор. Який практичний зміст? А сенс такий, що завдання аналітичної геометрії площа паралелограма часто знаходять через поняття векторного произведения:

Отримаємо другу важливу формулу. Діагональ паралелограма (червоний пунктир) ділить його на два рівні трикутники. Отже, площа трикутника, побудованого на векторах (червоне штрихування), можна знайти за формулою:

4) Не менш важливий факт полягає в тому, що вектор ортогональний векторам, тобто . Зрозуміло, протилежно спрямований вектор (малинова стрілка) теж ортогональний вихідним векторам.

5) Вектор спрямований так, що базисмає правуорієнтацію. На уроці про переході до нового базисуя досить докладно розповів про орієнтації площиниі зараз ми розберемося, що таке орієнтація простору. Пояснювати буду на ваших пальцях правої руки. Подумки поєднайте вказівний палецьз вектором і середній палецьз вектором. Безіменний палець та мізинецьпритисніть до долоні. В результаті великий палець- Векторний твір дивитися вгору. Це і є правоорієнтований базис (на малюнку саме він). Тепер поміняйте вектори ( вказівний та середній пальці) місцями, в результаті великий палець розгорнеться, і векторний твір уже дивитиметься вниз. Це також правоорієнтований базис. Можливо, у вас виникло питання: а який базис має ліву орієнтацію? "Привласніть" тим же пальцям лівої рукивектори , і отримайте лівий базис і ліву орієнтацію простору (у цьому випадку великий палець розташується у напрямку нижнього вектора). Образно кажучи, ці базиси «закручують» або орієнтують простір у різні боки. І це поняття не слід вважати чимось надуманим чи абстрактним – так, наприклад, орієнтацію простору змінює звичайнісіньке дзеркало, і якщо «витягнути відбитий об'єкт із дзеркалля», то його в загальному випадку не вдасться поєднати з «оригіналом». До речі, піднесіть до дзеркала три пальці та проаналізуйте відображення;-)

…як все-таки добре, що ви тепер знаєте про право- та лівоорієнтованихбазисах, бо страшні висловлювання деяких лекторів про зміну орієнтації =)

Векторний твір колінеарних векторів

Визначення докладно розібрано, залишилося з'ясувати, що відбувається, коли колінеарні вектори. Якщо вектори колінеарні, то їх можна розташувати на одній прямій і наш паралелограм теж складається в одну пряму. Площа такого, як кажуть математики, виродженогоПаралелограма дорівнює нулю. Це ж випливає і з формули - синус нуля або 180 градусів дорівнює нулю, а значить, і площа нульова

Таким чином, якщо , то і . Зверніть увагу, що саме векторний добуток дорівнює нульовому вектору, але на практиці цим часто нехтують і пишуть, що він також дорівнює нулю.

Окремий випадок – векторний твір вектора на самого себе:

За допомогою векторного твору можна перевіряти колінеарність тривимірних векторів, і це завдання серед інших ми теж розберемо.

Для вирішення практичних прикладів може знадобитися тригонометрична таблиця, щоб шукати значення синусів.

Ну що ж, розпалюємо вогонь:

Приклад 1

а) Знайти довжину векторного твору векторів, якщо

б) Знайти площу паралелограма, побудованого на векторах , якщо

Рішення: Ні, це не друкарська помилка, вихідні дані в пунктах умови я навмисно зробив однаковими. Тому що оформлення рішень відрізнятиметься!

а) За умовою потрібно знайти довжинувекторні (векторного твору). За відповідною формулою:

Відповідь:

Якщо питалося про довжину, то відповіді показуємо розмірність – одиниці.

б) За умовою потрібно знайти площапаралелограма, побудованого на векторах. Площа даного паралелограма чисельно дорівнює довжині векторного твору:

Відповідь:

Зверніть увагу, що у відповіді про векторний витвір не йдеться взагалі, нас запитували про площі фігуривідповідно розмірність - квадратні одиниці.

Завжди дивимося, що потрібно знайти за умовою, і, виходячи з цього, формулюємо чіткийвідповідь. Може здатися буквоїдством, але літероїдів серед викладачів вистачає, і завдання з добрими шансами повернеться на доопрацювання. Хоча це не особливо натягнута причіпка - якщо відповідь некоректна, то складається враження, що людина не розуміється на простих речах і/або не вникла в суть завдання. Цей момент завжди потрібно тримати на контролі, вирішуючи будь-яке завдання з вищої математики та й з інших предметів теж.

Куди поділася велика літера «ен»? В принципі, її можна було додатково приліпити до рішення, але з метою скоротити запис, я цього не зробив. Сподіваюся, всім зрозуміло, що і це позначення одного і того ж.

Популярний приклад для самостійного вирішення:

Приклад 2

Знайти площу трикутника, побудованого на векторах , якщо

Формула знаходження площі трикутника через векторний добуток дана в коментарях до визначення. Рішення та відповідь наприкінці уроку.

Насправді завдання справді дуже поширена, трикутниками взагалі можуть закатувати.

Для вирішення інших завдань нам знадобляться:

Властивості векторного твору векторів

Деякі властивості векторного твору ми вже розглянули, проте я їх включу до цього списку.

Для довільних векторів та довільного числа справедливі такі властивості:

1) В інших джерелах інформації цей пункт зазвичай не виділяють у властивостях, але він дуже важливий у практичному плані. Тож нехай буде.

2) - Властивість теж розібрано вище, іноді його називають антикомутативністю. Інакше кажучи, порядок векторів має значення.

3) - сполучні або асоціативнізакони векторної праці. Константи безпроблемно виносяться за межі векторного твору. Справді, чого їм робити?

4) - розподільні або дистрибутивнізакони векторної праці. З розкриттям дужок також немає проблем.

Як демонстрацію розглянемо коротенький приклад:

Приклад 3

Знайти , якщо

Рішення:За умовою знову потрібно знайти довжину векторного твору. Розпишемо нашу мініатюру:

(1) Згідно з асоціативними законами, виносимо константи за межі векторного твору.

(2) Виносимо константу межі модуля, у своїй модуль «з'їдає» знак «мінус». Довжина ж може бути негативною.

(3) Подальше зрозуміло.

Відповідь:

Настав час підкинути дров у вогонь:

Приклад 4

Обчислити площу трикутника, побудованого на векторах , якщо

Рішення: Площа трикутника знайдемо за формулою . Загвоздка у тому, що вектори «це» і «де» самі представлені як сум векторів. Алгоритм тут стандартний і чимось нагадує приклади №3 та 4 уроку Скалярне твір векторів. Рішення для ясності розіб'ємо на три етапи:

1) На першому кроці висловимо векторний твір через векторний твір, по суті, виразимо вектор через вектор. Про довжини поки що ні слова!

(1) Підставляємо вирази векторів.

(2) Використовуючи дистрибутивні закони, розкриваємо дужки за правилом множення багаточленів.

(3) Використовуючи асоціативні закони, виносимо всі константи за межі векторних творів. При малому досвіді дії 2 і 3 можна виконувати одночасно.

(4) Перше та останнє доданок дорівнює нулю (нульовому вектору) завдяки приємній властивості. У другому доданку використовуємо властивість антикомутативності векторного твору:

(5) Наводимо подібні доданки.

В результаті вектор виявився через вектор, чого і потрібно досягти:

2) На другому етапі знайдемо довжину необхідного нам векторного твору. Ця дія нагадує Приклад 3:

3) Знайдемо площу шуканого трикутника:

Етапи 2-3 рішення можна було оформити і одним рядком.

Відповідь:

Розглянуте завдання досить поширене у контрольних роботах, ось приклад для самостійного вирішення:

Приклад 5

Знайти , якщо

Коротке рішеннята відповідь наприкінці уроку. Подивимося, наскільки ви були уважні щодо попередніх прикладів;-)

Векторний твір векторів у координатах

, заданих в ортонормованому базисі , виражається формулою:

Формула і справді простецька: у верхній рядок визначника записуємо координатні вектори, у другий і третій рядки «укладаємо» координати векторів, причому укладаємо у строгому порядку- Спершу координати вектора "ве", потім координати вектора "дубль-ве". Якщо вектори потрібно помножити в іншому порядку, то рядки слід поміняти місцями:

Приклад 10

Перевірити, чи колінеарні будуть наступні вектори простору:
а)
б)

Рішення: Перевірка заснована на одному із тверджень даного уроку: якщо вектори колінеарні, то їхній векторний добуток дорівнює нулю (нульовому вектору): .

а) Знайдемо векторний твір:

Таким чином, вектори не колінеарні.

б) Знайдемо векторний твір:

Відповідь: а) не колінеарні; б)

Ось, мабуть, і всі основні відомості про векторні твори векторів.

Цей розділ буде невеликим, оскільки завдань, де використовується змішане твір векторів, небагато. Практично все буде впиратися у визначення, геометричний зміст і кілька робочих формул.

Змішаний твір векторів – це твір трьохвекторів:

Ось так вони вишикувалися паровозиком і чекають, не дочекаються, коли їх обчислять.

Спочатку знову визначення та картинка:

Визначення: Змішаним твором некомпланарнихвекторів, взятих у даному порядку, називається обсяг паралелепіпеда, побудованого на даних векторах, з знаком «+», якщо базис правий, і знаком «–», якщо базис лівий.

Виконаємо малюнок. Невидимі нам лінії прокреслені пунктиром:

Занурюємося у визначення:

2) Вектори взяті у певному порядку, тобто перестановка векторів у творі, як ви здогадуєтеся, не минає без наслідків.

3) Перед тим, як прокоментувати геометричний зміст, зазначу очевидний факт: змішаний твір векторів є ЧИСЛОМ: . У навчальній літературі оформлення може бути дещо іншим, я звик позначати змішане твір через , а результат обчислень літерою «пе».

За визначенням змішаний твір – це обсяг паралелепіпеда, побудованого на векторах (фігура прокреслена червоними векторами та лініями чорного кольору). Тобто число дорівнює обсягу даного паралелепіпеда.

Примітка : креслення є схематичним.

4) Не заново паритися з поняттям орієнтації базису та простору. Сенс заключної частини у тому, що до обсягу може додаватися знак мінус. Простими словами, змішане твір може бути негативним: .

Безпосередньо з визначення слідує формула обчислення об'єму паралелепіпеда, побудованого на векторах.

Визначення. Векторним твором вектора а на вектор b називається вектор, що позначається символом [«, Ь] (або л х Ь), такий, що 1) довжина вектора [а, b] дорівнює (р, де у - кут між векторами а і b ( 2) вектор [а, Ь) перпендикулярний векторам а і Ь, тобто. перпендикулярний площині цих векторів; 3) вектор [а, Ь] спрямований так, що з кінця цього вектора найкоротший поворот від а до b видно тим, що відбувається проти годинникової стрілки (рис. 32). Рис. 32 Рис.31 Інакше кажучи, вектори a, b і [а,Ь) утворюють праву трійку векторів, тобто. розташовані так, як великий, вказівний та середній пальці правої руки. У разі, якщо вектори а і b колінеарні, будемо вважати, що [а, Ь] = 0. За визначенням довжина векторного твору чисельно дорівнює площі Sa паралелограма (рис. 33), побудованого на векторах, що перемножуються, а і b як на сторонах: 6.1 . Властивості векторного твору 1. Векторний добуток дорівнює нульовому вектору тоді і тільки тоді, коли принаймні один з векторів, що перемножуються, є нульовим або коли ці вектори колінеарні (якщо вектори а і b колінеарні, то кут між ними дорівнює або 0, або 7г). Це легко отримати з того, що Якщо вважати нульовий вектор коллінсарним будь-якому вектору, то умова колінеарності векторів а і b можна висловити так 2. Векторний твір антикоммутативно, тобто завжди. Справді, вектори (а, Ь) мають однакову довжину і колінеарні. Напрямки цих векторів протилежні, оскільки з кінця вектора [а, Ь] найкоротший поворот від а до b буде видно тим, що відбувається проти годинникової стрілки, а з кінця вектора [Ь, а] - за годинниковою стрілкою (рис. 34). 3. Векторний твір має розподільну властивість до додавання 4. Числовий множник Л можна виносити за знак векторного твору 6.2. Векторний витвір векторів, заданих координатами Нехай вектори а та Ь задані своїми координатами у базисі. Користуючись розподільною властивістю векторного твору, знаходимо векторний добуток заданих координатами. Змішане твір. Випишемо векторні твори координатних ортів (рис. 35): Тому для векторного твору векторів а і b отримуємо з формули (3) такий вираз Формулу (4) можна записати в символічній формі, що легко запам'ятовується, якщо скористатися визначником 3-го порядку: Розкладаючи цей визначник за елементами 1-го рядка, отримаємо (4). приклади. 1. Знайти площу паралелограма, побудованого на векторах Шукана площа Тому знаходимо = звідки 2. Знайти площу трикутника (рис. 36). Зрозуміло, що площа б"д трикутника ВАТ дорівнює половині площі S паралелограма О АС В. Обчислюючи векторний твір (а, Ь| векторів а = OA і b = оЪ, отримуємо Звідси Зауваження. Векторний твір не асоціативно, тобто рівність (а, Ь),с) = [а, |Ь,с)) у загальному випадку неправильно Наприклад, при а = ss j маємо § 7. Змішаний добуток векторів Нехай маємо три вектори а, Ь і с. і 1> вкторно В результаті отримаємо вектор [а, 1>] Помножимо його скалярно на вектор з: (к Ь), с) Число ([а, Ь], е) називається змішаним твором векторів а, Ь. с і позначається символом (а, 1), е) 7.1 Геометричний сенс змішаного твору Відкладемо вектори а, b і з точки, що відійшла (рис. 37) Якщо всі чотири точки О, А, В, С лежать в одній площині ( вектори a, b і с називаються в цьому випадку компланарними), то змішане твір ([а, Ь], с) = 0. Це випливає з того, що вектор [а, Ь|перпендикулярний до площини, в якій лежать вектори а і 1 », а значить, і вектору с./ Якщо ж т окуляри О, А, В, С не лежать в одній плоскості (вектори a, b і з некомпланарні), побудуємо на ребрах OA, OB та ОС паралелепіпед (рис. 38 а). За визначенням векторного твору маємо (a,b) = So, де So - площа паралелограма OADB, а з - одиничний вектор, перпендикулярний векторам а і Ь і такий, що трійка а, Ь, с - права, тобто. вектори a, b та с розташовані відповідно як великий, вказівний та середній пальці правої руки (рис. 38 б). Помножуючи обидві частини останньої рівності справа скалярно на вектор, отримуємо, що векторний добуток векторів заданих координатами. Змішане твір. Число ргс дорівнює висоті h побудованого паралелепіпеда, взятого зі знаком «+», якщо кут між векторами с і з гострий (трійка а, Ь, с - права), і зі знаком «-», якщо кут - тупий (трійка а, Ь, с - ліва), так що Тим самим, змішаний добуток векторів а, Ь і з дорівнює обсягу V паралелепіпеда, побудованого на цих векторах як на ребрах, якщо трійка а, Ъ, с - права, і -V, якщо трійка а , Ь, с – ліва. Виходячи з геометричного сенсу змішаного твору, можна зробити висновок, що, перемножуючи тс ж вектори a, b і з будь-якому іншому порядку, ми завжди будемо отримувати або +7, або -К. Знак вироб- Рис. 38 ведення залежатиме лише від того, яку трійку утворюють вектори, що перемножуються, - праву або ліву. Якщо вектори а, Ь, утворюють праву трійку, то правими будуть також трійки Ь, с, а і с, а, Ь. У той самий час всі три трійки Ь, а, з; а, с, Ь і с, Ь, а – ліві. Тим самим, (а,Ь, с) = (Ь,с, а) = (с,а,Ь) = -(Ь,а,с) = -(а,с,Ь) = -(с,Ь а). Ще раз підкреслимо, що змішане твір векторів одно нулютоді тільки тоді, коли перемножуються вектори а, Ь, з компланарні: (а, Ь, з компланарні) 7.2. Змішаний твір у координатах Нехай вектори а, Ь, із заданими своїми координатами в базисі i, j, k: а = (x\,y\,z]), b=(x2,y2>z2), c = (х3, уз,23). Знайдемо вираз їхнього змішаного твори (а, Ь, з). Маємо змішане твір векторів, заданих своїми координатами в базисі i, J, до, дорівнює визначнику третього порядку, рядки якого складені відповідно з координат першого, другого та третього з векторів, що перемножуються. Необхідна та достатня умова компланарності векторів а у\, Z|), b = (хъ У2. 22), с = (жз, уз, 23) запишеться у такому вигляді У | z, аг2 у2 -2 = 0. Вуз Приклад. Перевірити, чи є компланарними вектори „ = (7,4,6), Ь = (2, 1,1), с = (19, II, 17). Вектори, що розглядаються, будуть компланарні або некомпланарні залежно від того, дорівнюватиме нулю чи ні визначник Розкладаючи його за елементами першого рядка, отримаємо Д = 7- 6- 4- 15 + 6-3 = 0^- вектори n, Ь, з компланарними. 7.3. Подвійне векторний твір Подвійний векторний твір [а, [Ь, с]] є вектором, перпендикулярним до векторів а і [Ь, с]. Тому він лежить у площині векторів b і с і може бути розкладений цими векторами. Можна показати, що справедлива формула [а, [!>, с]] = Ь(а, е) - с(а, Ь). Вправи 1. Три вектори АВ = с, Ж? = про СА = b служать сторонами трикутника. Виразити через a, b і вектори, що збігаються з медіанами AM, DN, CP трикутника. 2. Якою умовою мають бути пов'язані вектори р і q, щоб вектор р + q ділив кут між ними навпіл? Передбачається, що всі три вектори віднесені до загального початку. 3. Обчисліть довжину діагоналей паралелограма, побудованого на векторах а = 5р + 2q та b = р - 3q, якщо відомо, що |р| = 2v/2, | q | = 3 H-(p7ci) = f. 4. Позначивши через а та b сторони ромба, що виходять із загальної вершини, доведіть, що діагоналі ромба взаємно перпендикулярні. 5. Обчисліть скалярний добуток векторів а = 4i + 7j + 3k та b = 31 - 5j + k. 6. Знайдіть одиничний вектор а0, паралельний вектору а = (6, 7, -6). 7. Знайдіть проекцію вектора a = l + j-kHa вектор b = 21 - j - 3k. 8. Знайдіть косинус кута між векторами IS «ж, якщо А(-4,0,4), В(-1,6,7), С(1,10.9). 9. Знайдіть одиничний вектор р°, одночасно перпендикулярний вектору а = (3, 6, 8) та осі Ох. 10. Обчисліть синус кута між діагоналями паралелофама, побудованого на векторах a = 2i+J-k, b=i-3j + k як на сторонах. Обчисліть висоту h паралелепіпеда, побудованого на векторах а = 31 + 2j - 5k, b = i-j + 4knc = i-3j + к, якщо за основу взято паралелограм, побудований на векторах а та I). Відповіді

Визначення. Векторним твором вектора а (множинне) на колінеарний йому вектор (множник) називається третій вектор з (твір), який будується наступним чином:

1) його модуль чисельно дорівнює площі паралелограма на рис. 155), побудованого на векторах тобто він дорівнює напрям перпендикулярно площині згаданого паралелограма;

3) при цьому напрям вектора з вибирається (з двох можливих) так, щоб вектори складали праву систему (§ 110).

Позначення: або

Доповнення до визначення. Якщо вектори колінеарні, то фігурі вважаючи її (умовно) паралелограмом, звичайно приписати нульову площу. Тому векторний добуток колінеарних векторів вважається рівним нуль-вектору.

Оскільки нуль-вектору можна приписати будь-який напрямок, ця угода не суперечить пунктам 2 та 3 визначення.

Зауваження 1. У терміні «векторний твір» перше слово вказує на те, що результат дії є вектором (на противагу скалярному твору; порівн. § 104, зауваження 1).

Приклад 1. Знайти векторний твір, де основні вектори правої системи координат (рис. 156).

1. Оскільки довжини основних векторів дорівнюють одиниці масштабу, то площа паралелограма (квадрату) чисельно дорівнює одиниці. Отже, модуль векторного добутку дорівнює одиниці.

2. Оскільки перпендикуляр до площини є ось, то шуканий векторний твір є вектор, колінеарний вектору до; бо обидва вони мають модуль 1, то шуканий векторний добуток дорівнює або k, або -k.

3. З цих двох можливих векторів треба вибрати перший, тому що вектори утворюють праву систему (а вектори ліву).

Приклад 2. Знайти векторний твір

Рішення. Як приклад 1, укладаємо, що вектор дорівнює або k, або -k. Але тепер треба вибрати -k, тому що вектори утворюють праву систему (а вектори ліву). Отже,

Приклад 3. Вектори мають довжини відповідно рівні 80 і 50 см, і утворюють кут 30°. Взявши за одиницю довжини метр, знайти довжину векторного твору

Рішення. Площа паралелограма, побудованого на векторах дорівнює Довжина шуканого векторного твору дорівнює

Приклад 4. Знайти довжину векторного твору тих самих векторів, взявши за одиницю довжини сантиметр.

Рішення. Оскільки площа паралелограма, побудованого векторах дорівнює то довжина векторного добутку дорівнює 2000 див, тобто.

З порівняння прикладів 3 і 4 видно, що довжина вектора залежить як від довжин сомножителей але і від вибору одиниці довжини.

Фізичний сенс векторного твору.З численних фізичних величин, що зображуються векторним твором, розглянемо лише момент сили.

Нехай А є точка докладання сили Моментом сили щодо точки О називається векторний твір Оскільки модуль цього векторного твору чисельно дорівнює площі паралелограма (рис. 157), то модуль моменту дорівнює добутку підстави на висоту, тобто силі, помноженій на відстань від точки О до прямої, вздовж якої діє сила.

У механіці доводиться, що з рівноваги твердого тіла необхідно, щоб дорівнювала нулю як сума векторів , які мають сили, прикладені до тіла, але й сума моментів сил. У тому випадку, коли всі сили паралельні одній площині, складання векторів, що представляють моменти, можна замінити додаванням та відніманням їх модулів. Але за довільних напрямів сил така заміна неможлива. Відповідно до цього векторний твір визначається саме як вектор, а не як число.

Векторний витвір- це псевдовектор, перпендикулярний до площини, побудованої по двох співмножниках, що є результатом бінарної операції «векторне множення» над векторами в тривимірному Евклідовому просторі. Векторний твір не має властивостей комутативності та асоціативності (є антикомутативним) і, на відміну від скалярного твору векторів, є вектором. Широко використовується в багатьох технічних та фізичних додатках. Наприклад, момент імпульсу і сила Лоренца математично записуються як векторного произведения. Векторний добуток корисний для «вимірювання» перпендикулярності векторів - модуль векторного твору двох векторів дорівнює добутку їх модулів, якщо вони перпендикулярні, і зменшується до нуля, якщо вектори паралельні або антипаралельні.

Визначити векторний твір можна по-різному, і теоретично, у просторі будь-якої розмірності n можна обчислити твір n-1 векторів, отримавши у своїй єдиний вектор, перпендикулярний до них всім. Але якщо твір обмежити нетривіальними бінарними творами з векторними результатами, то традиційний векторний твір визначено лише у тривимірному та семимірному просторах. Результат векторного твору, як і скалярного, залежить від метрики Евклідова простору.

На відміну від формули для обчислення за координатами векторів скалярного твору в тривимірній прямокутній системі координат, формула для векторного твору залежить від орієнтації прямокутної системи координат або інакше її «хіральності».

Визначення:
Векторним добутком вектора a на вектор b у просторі R 3 називається вектор c , що відповідає наступним вимогам:
довжина вектора c дорівнює добутку довжин векторів a та b на синус кута φ між ними:
|c|=|a||b|sin φ;
вектор c ортогональний кожному з векторів a та b;
вектор c спрямований так, що трійка векторів abc є правою;
у разі простору R7 потрібна асоціативність трійки векторів a, b, c.
Позначення:
c===a × b

Рис. 1. Площа паралелограма дорівнює модулю векторного твору

Геометричні властивості векторного твору:
Необхідною та достатньою умовою колінеарності двох ненульових векторів є рівність нуля їхнього векторного твору.

Модуль векторного твору дорівнює площі Sпаралелограма, побудованого на приведених до загального початку векторах aі b(Див. рис.1).

Якщо e- одиничний вектор, ортогональний вектор aі bі вибраний так, що трійка a,b,e- права, а S- площа паралелограма, побудованого на них (наведених до загального початку), то для векторного твору справедлива формула:
=S e

Рис.2. Об'єм паралелепіпеда при використанні векторного та скалярного твору векторів; пунктирні лінії показують проекції вектора c на a × b та вектора a на b × c, першим кроком є ​​знаходження скалярних творів

Якщо c- якийсь вектор, π - будь-яка площина, що містить цей вектор, e- одиничний вектор, що лежить у площині π і ортогональний до c,g- одиничний вектор, ортогональний до площини π і спрямований так, що трійка векторів ecgє правою, то для будь-кого, хто лежить у площині π вектора aсправедлива формула:
=Pr e a |c|g
де Pr e a проекція вектора e на a
|c|-модуль вектора з

При використанні векторного та скалярного творів можна вирахувати обсяг паралелепіпеда, побудованого на приведених до загального початку векторах a, bі c. Таке твір трьох векторів називається змішаним.
V=|a (b×c)|
На малюнку показано, що цей обсяг може бути знайдений двома способами: геометричний результат зберігається навіть при заміні «скалярного» та «векторного» творів подекуди:
V=a×b c=a b×c

Величина векторного твору залежить від синуса кута між первісними векторами, тому векторний твір може сприйматися як ступінь перпендикулярності векторів так само, як і скалярний твір може розглядатися як ступінь паралельності. Векторний добуток двох одиничних векторів дорівнює 1 (одиничному вектору), якщо початкові вектори перпендикулярні, і дорівнює 0 (нульовому вектору), якщо вектори паралельні або антипаралельні.

Вираз для векторного твору в декартових координатах
Якщо два вектори aі bвизначені своїми прямокутними декартовими координатами, а точніше - представлені в ортонормованому базисі
a = (a x, a y, a z)
b = (b x, b y, b z)
а система координат права, то їхній векторний твір має вигляд
=(a y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
Для запам'ятовування цієї формули:
i = ∑ε ijk a j b k
де ε ijk- символ Леві-Чівіти.