Predtým, ako chápeme tvorbu vektorov, prejdeme k nutričnej orientácii usporiadanej trojice vektorov a → , b → , c → v triviálnom priestore.

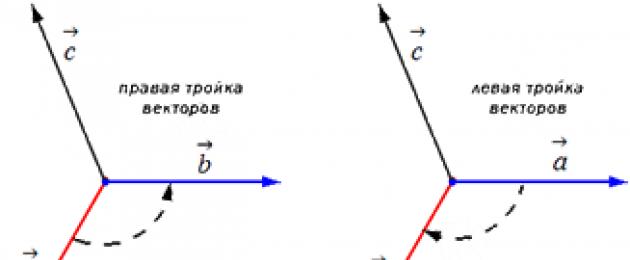
Vektory a → , b → , c → sčítame ako jeden bod. Orientácia triády a → , b → , c → je vpravo alebo vľavo, v súlade so smerom samotného vektora c → . Okrem toho, ktorým smerom je najkratšia odbočka z vektora a → do b → od konca vektora c → určí sa typ triády a → , b → , c →.

Ak nastane najkratšia rotácia oproti šípke letopočtu, potom sa nazýva trojica vektorov a → , b → , c → správny, hneď za šípkou výročia - Levi.

Ďalej vezmeme dva nekolineárne vektory a → a b → . Potom pridáme vektory AB → = a → a A C → = b → z bodu A. Predpokladajme, že vektor A D → = c → je kolmý na і A B → і A C → . Keď nás teda vyzve samotný vektor A D → = c →, môžeme ho nájsť nezávisle a pýtať sa buď priamo, alebo naopak (pozri obrázok).

Tri vektory a → , b → , c → môžu byť usporiadané, ako sme vysvetlili s pravou rukou a ľavou stranou v súlade so smerom vektora.

S vyššie uvedeným si môžeme predstaviť význam tvorby vektorov. Táto hodnota je daná pre dva vektory, priradené k pravouhlému súradnicovému systému triviálneho priestoru.

Viznachennya 1

Vektorové vytvorenie dvoch vektorov a → a b → Takýto vektor úloh v priamočiarom súradnicovom systéme triviálneho priestoru nazývame taký, že:

• Ak sú vektory a → a b → kolineárne, budú nulové;
• Bude kolmý na vektor a → a vektor b → rovnaký. ∠ a → c → ∠ b → c → = π 2 ;
• Tento dovzhin je určený vzorcom: c → = a → · b → · sin ∠ a → , b →;
• Trojica vektorov a → , b → , c → má rovnakú orientáciu ako je zadaný súradnicový systém.

Vektorové sčítanie vektorov a → a b → má rovnaký význam: a → × b → .

Súradnice vektorového umenia

Ak ktorýkoľvek vektor obsahuje špecifické súradnice v súradnicovom systéme, môžete zadať inú hodnotu pre vytvorenie vektora, ktorá vám umožní nájsť jeho súradnice za danými súradnicami vektorov.

Vicennia 2

V pravouhlom súradnicovom systéme triviálneho priestoru vektorová tvorba dvoch vektorov a → = (a x ; a y ; a z) і b → = (b x ; b y ; b z) volajme vektor c → = a → × b → = (ay bz - az by) i → + (az bx - ax bz) j → + (ax by - ay bx) k → , kde i → j → k → є súradnicové vektory.

Vektorové teleso môže byť reprezentované ako derivácia štvorcovej matice tretieho rádu, pričom prvý riadok sú ori vektory i → , j → , k → , ďalší riadok obsahuje súradnice vektora a → a tretí riadok obsahuje súradnice vektora b → ak je daný pravouhlý súradnicový systém, áno, znak matice vyzerá takto: c → = a → × b → = i → j → k → axayazbxbybz

Po rozdelení prvého riadku na prvky prvého radu sa žiarlivosť odstráni: j → k → axayazbxbybz = ayazbybz · i → - axazbxbz · j → + axaybxby · k → = = a → × b → = (ay · bz - az · by) i → + (az · bx - ax · bz) · j → + (ax · by - ay · bx) · k →

Sila vektorového umenia

Zdá sa, že vektorové teleso v súradniciach je reprezentované ako primárna matica c → = a → × b → = i → orgány vedúceho matice sa javí takto sila tvorby vektorov:

1. antikomutatívnosť a → × b → = - b → × a →;
2. distributivita a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → alebo a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. asociativita λ · a → × b → = λ · a → × b → alebo a → × (λ · b →) = λ · a → × b → , kde λ je efektívnejšie číslo.

Tieto autority predkladajú zložité dôkazy.

Napríklad do vektorovej tvorby môžeme vniesť silu antikomutatívnosti.

Dôkaz antikomutativity

Pre významy a → x b → = i → j → k → a x a y z b x b y b z і b → x a → = i → j → k → b x b y b z a x a y a z . A ak sú dva riadky matice preusporiadané, potom sa hodnoty primárnej matice môžu zmeniť na strane, takže a → x b → = i → j → k → axayazbxbybz = - i → j → k → bxbybzaxayaz = - b → × a → a priniesť antikomutatívne vektorové umenie.

Vector tvir – aplikácia a riešenie

Najčastejšie ide o tri typy objednávok.

Pri úlohách prvého typu priraďte úlohy dvom vektorom a medzi nimi a potrebujete poznať hodnotu vytvorenia vektora. V tomto prípade sa používa nasledujúci vzorec: c → a → b → sin ∠ a → , b → .

zadok 1

Nájdite maximálnu hodnotu vektorových vektorov a → a b →, keďže vieme a → = 3, b → = 5, ∠ a →, b → = π 4.

rozhodnutie

Pre dodatočnú hodnotu vektorovej tvorby vektorov a → a b → je problém jasne daný: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

Predmet: 15 2 2 .

Problémy iného typu súvisia so súradnicami vektorov, niektorými vektormi a pod. hľadať cez vonkajšie súradnice zadaných vektorov a → = (a x; a y; a z) і b → = (b x ; b y ; b z) .

Pre tento typ objednávky si môžete vybrať z mnohých možností objednávky. Napríklad súradnice vektorov a → a b → nemusia byť špecifikované, ale sú usporiadané podľa súradnicových vektorov tvaru b → = b x · i → + b y · j → + b z · k → і c → = a → × b → = (ay · bz - az · by) · i → + (az · bx - ax · bz) · j → vektory a → a b → môžu byť špecifikované súradnicami bodov ix a koniec.

Pozrime sa na tieto príklady.

zadok 2

Priamočiaremu súradnicovému systému sú dané dva vektory a → = (2; 1; - 3), b → = (0; - 1; 1). Nájdite svoj vektorový televízor.

rozhodnutie

Pre iné významy poznáme vektorové sčítanie dvoch vektorov na daných súradniciach: a → × b → = (ay · bz - az · by) · i → + (az · bx - ax · bz) · j → + (ax · by - ay · bx) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2 · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .

Ak zapíšete vektorovú TV cez primárnu maticu, potom riešenie tohto problému vyzerá takto: a → x b → = i → j → k → axayazbxbybz = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Predmet: a → × b → = - 2 i → - 2 j → - 2 k → .

zadok 3

Nájdite holubicu vektorového vektora i → - j → a i → + j → + k → , kde i → , j → , k → - ori pravouhlého karteziánskeho súradnicového systému.

rozhodnutie

Pre klas poznáme súradnice daného vytvorenia vektora i → - j → × i → + j → + k → v tomto priamočiarom súradnicovom systéme.

Zdá sa, že vektory i → - j → і i → + j → + k → posúvajú súradnice (1; - 1; 0) і (1; 1; 1) podobným spôsobom. Poznáme hodnotu vytvorenia vektora za pomocou maticového signifikátora, takže môžeme i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Taktiež vektorové teleso i → - j → × i → + j → + k → posúva súradnice (-1; - 1; 2) v danom súradnicovom systéme.

Dovzhin tvorby vektora je známy podľa vzorca (delenie dovzhin vektora): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

Predmet: i → - j → × i → + j → + k → = 6 . .

zadok 4

Pravouhlý kartézsky súradnicový systém má zadané tri súradnice: A (1, 0, 1), B (0, 2, 3), C (1, 4, 2). Nájdite ľubovoľný vektor kolmý na A B → і A C → jedna hodina.

rozhodnutie

Vektory A B → і A C → posúvajú dopredu súradnice (- 1 ; 2 ; 2) a (0 ; 4 ; 1) rovnakým spôsobom. Keď poznáme sčítanie vektorov A B → a A C →, je zrejmé, že ide o kolmý vektor za hodnotami i k A B → a k A C →, potom vyriešime náš problém. Vieme to A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Predmet: - 6 i → + j → - 4 k → . - jeden z kolmých vektorov.

Úloha tretieho typu je orientovaná na vikoristán síl vektorovej tvorby vektorov. Po stagnácii budeme pokračovať v rozhodovaní o danej úlohe.

zadok 5

Vektory a → ta b → kolmé na ix a na rovnakú úroveň ako 3 a 4. Nájdite polovicu tvorby vektora 3 · a → - b → × a → - 2 · b → = 3 · a → × a → - 2 · b → + - b → × a → - 2 · b → = = 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .

rozhodnutie

Pre silu distributivity tvorby vektorov môžeme napísať 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Intenzita asociatívnosti je spôsobená číselným koeficientom pre znamienko vektorových výtvorov vo zvyšnom výraze: 3 a → × a → 3 a → = 3 a → × a → + 3 (- 2) a → × b → + ( - 1 ) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b →

Vytvorenie vektora a → × a → і b → × b → rovná sa 0, fragmenty a → × a → = a → · a → · sin 0 = 0 и b → × b → = b → · b → 0, potom 3 · a → × a → - 6 · a → × b → - b → ? .

V dôsledku antikomutatívnosti tvorby vektora je to - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × b → . .

Keďže sme boli oživení silami tvorenia vektorov, odmietame žiarlivosť 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

Za mysľou sú vektory a → a b → kolmé, takže medzi nimi je spoločné π 2 . Teraz už nie je možné nahradiť nájdené hodnoty v nasledujúcom vzorci: 3 · a → - b → ? → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .

Predmet: 3 a → - b → × a → - 2 b → = 60.

Zdvojnásobenie vektorovej tvorby vektorov za poradím je a → × b → = a → · b → · sin ∠ a → , b → . Fragmenty sú už známe (zo školského kurzu), plocha trikutnika sa rovná polovici dvoch strán dowzhin vynásobených sínusom kut medzi týmito stranami. Druhá strana vektora je tiež plochý rovnobežník - podkožné trikubitule a ostatné strany samotné vyzerajú ako vektory a → a b → rozkladajúce jeden bod na sínuse rezu medzi nimi sin ∠ a → , b → .

Toto je geometrický zmysel vytvárania vektorov.

Fyzický zmysel pre tvorbu vektorov

V mechanike, jednom z odvetví fyziky, je možné použiť vektorovú tvorbu na určenie momentu sily v bode priestoru.

Vicenzennya 3

Pod momentom sily F → pôsobiacej na bod B, pred bodom A je rozumné predpokladať nástup vektorovej sily A B → × F →.

Ak ste v texte označili láskavosť, pozrite si ju a stlačte Ctrl+Enter

V tejto lekcii sa pozrieme na ďalšie dve operácie s vektormi: vektorové dodatočné vektoryі zmiešané pevné vektory (okamžite odoslané tým, ktorí to potrebujú). Nevadí, niekedy sa to stane, takže pre väčšie šťastie krém skalárne vytváranie vektorov, Potrebujete viac a viac. Toto je vektorová os drogovej závislosti. Môžeme sa stať nepriateľskými voči skutočnosti, že stúpame do troch analytických geometrií. Nie tak. Táto časť vysokopostavených matematikov má málo dreva na brúsenie na Pinocchia. V skutočnosti je materiál ešte širší a jednoduchší – sotva zložitejší ako ten istý skalárny tvir, bude pravdepodobne menej typických úloh. Golovne v analytickej geometrii, keďže mnohí, ktorí sú konvertovaní alebo už konvertovaní, NEMAJÚ Zľutovanie s HIV PLÁNMI. Opakujte ako kúzlo a budete šťastní.

Keďže vektory vibrujú tu ďaleko, ako záblesky na obzore, nezáleží na tom, začnime s lekciou Vektory pre figuríny, aktualizovať alebo získať základné vedomosti o vektoroch. Pripravenejší čitatelia sa môžu zoznámiť s vybranými informáciami, snažil som sa zozbierať čo najširšiu zbierku aplikácií, ktoré sa často nachádzajú v praktických robotoch

Ako ťa môžem urobiť šťastným? Keď som bol malý, vedel som žonglovať s dvoma ľuďmi a nosiť tri tašky. Vyšlo to rýchlo. Nebudete môcť neustále žonglovať, pokiaľ vidíme iba priestranné vektory a rovinné vektory z dvoch súradníc sa stratia cez palubu. prečo? Takto sa už zrodili dáta – vektory a zmesi pevných vektorov sú označené a fungujú v triviálnom priestore. Je to jednoduchšie!

Táto operácia, rovnako ako pri skalárnom vytváraní, sa zúčastňuje dva vektory. Nech existujú nezničiteľné písmená.

Samotná akcia znamenalo Poďme dopredu s hodnosťou: . Existujú aj iné možnosti, ale vektor nazvem ako pevné vektory so štvorcovými ramenami s krížikom.

ja okamžite jedlo: kde je skalárne vytváranie vektorov vezmite osud dvoch vektorov a potom sa dva vektory tiež vynásobia aký je rozdiel? Rozdiel je zrejmý v prvom rade vo výsledku:

Výsledok skalárnej tvorby vektorov є:

Výsledkom tvorby vektora je VECTOR: , potom sa vektor vynásobí a vektor sa opäť odčíta. Uzavretý klub. Vlasna, to je názov prevádzky. Na Riznom základná literatúra Označenia môžu byť tiež rôzne, zmením písmeno .

Dizajn vektorového umenia

Najprv bude obrázok, potom komentár.

Viznachennya: Vektorové umenie nekolineárne vektory, prevzaté z tejto objednávky s názvom VECTOR, dovzhinačo číselne staroveký rovnobežník štvorec na základe týchto vektorov; vektor ortogonálne k vektorom a narovnanie tak, aby mal základ správnu orientáciu:

Poďme to vyriešiť štetcom, je tu veľa dobrých vecí!

No môžeme vymenovať také podstatné momenty:

1) Výstupné vektory označené červenými šípkami za označenými nie kolineárne. Rozdelenie kolineárnych vektorov bude diskutované o niečo neskôr.

2) Nasnímané vektory v prísnom poradí: – "a" vynásobte "byť" a chi nie je „byť“ s „a“. Výsledok násobenia vektorovє Vektor, ktorý je označený modrou farbou. Ak sa vektory vynásobia v opačnom poradí, odstráni sa rovnaký vektor za dowzhin a predĺžený vektor v priamom vektore (malinová farba). To je správna žiarlivosť .

3) Teraz je to známe z geometrickej polohy vytvorenia vektora. Toto je mimoriadne dôležitý bod! Plocha modrého vektora (a tiež karmínového vektora) je číselne väčšia ako PLOCHA rovnobežníka nakresleného na vektoroch. Malý má rovnobežník tieňovania v čiernej farbe.

Poznámka : stolička je schematická a, prirodzene, nominálna hodnota vektorového výtvoru nie je porovnateľná s rovinou rovnobežníka.

Uhádnime jeden z geometrických vzorcov: plocha rovnobežníka je relatívnym pridaním susedných strán k sínusu rezu medzi nimi. Preto na základe toho, čo bolo povedané, platí vzorec na výpočet DOVHINI tvorby vektorov:

Chcel by som zdôrazniť, že vzorec je o DVOJNÁSOBKU vektora, a nie o vektore samotnom. Aká praktická zmena? A zmysel je, že znalosť analytickej geometrie oblasti rovnobežníka sa často nachádza prostredníctvom konceptu vektorového produktu:

Odmietame dôležitú formulku priateľovi. Uhlopriečka rovnobežníka (červená bodkovaná čiara) ho rozdeľuje na dve trikutánne roviny. Takže štvorec tricutnika nakreslený na vektoroch (šrafovanie chervonov) možno nájsť podľa vzorca:

4) Nemenej dôležitý fakt spočíva v tom, že vektor je ortogonálny k vektorom . Je zrejmé, že rektifikačný vektor (karmínová šípka) je tiež ortogonálny k výstupným vektorom.

5) Vektor rektifikácií tak, aby základ smieť zákona orientácia. V triede o prejsť na nový základ Budem vás informovať o orientácia roviny A teraz zistíme, aká je táto orientácia na priestor. Vysvetlím ti to na prstoch pravá ruka. Jedzte svoje myšlienky vulgárny prst s vektorom i prostredník s vektorom. Prstenník a malíček stlačiť na dno. Ako výsledok veľký prst na nohe- Vector TV žasne nad horou. Toto je základ správnej orientácie (v najmenšej miere). Teraz zmeňte vektory ( Ležérny a prostredník) prerušovane, v dôsledku toho sa palec rozsvieti a vektorové telo sa už bude pohybovať nadol. To je tiež základ správnej orientácie. Možno máte problém s výživou: aký základ má ľavicová orientácia? „Aplikujte“ rovnakými prstami ľavá ruka vektory a zoberte ľavú základňu a ľavú orientáciu priestoru (v tomto prípade sa veľký prst tiahne priamo zo spodného vektora). Obrazne povedané, tieto základne sú „skrútené“ alebo je priestor orientovaný na rôzne strany. A tento koncept nemá byť ani pritažený za vlasy, ani abstraktný – napríklad orientácia priestoru zmení pôvodné zrkadlo a ak „vytiahnete predmet zo zrkadla“, nebudete môcť jesť s pôvodné". Pred rozprávaním položte tri prsty pred zrkadlo a analyzujte obraz ;-)

...je stále dobré, že o tom teraz viete orientované vpravo a vľavo základne, pretože je desivé počuť od niektorých lektorov o zmene orientácie =)

Vektorový súbor kolineárnych vektorov

O hodnote správy sa diskutovalo, nebolo možné pochopiť, čo sa očakáva, ak sú vektory kolineárne. Keďže vektory sú kolineárne, dajú sa rozšíriť na jednej priamke a náš rovnobežník sa tiež rozvinie do jednej priamky. Táto oblasť, ako sa zdá matematikom, virogén Rovnobežník sa rovná nule. Vyplýva to zo vzorca - sínus nuly alebo 180 stupňov sa rovná nule, čo znamená, že plocha je nula

Týmto spôsobom, ako to teda je і . Upozorňujeme, že samotný vektorový vstup je rovnako dobrý ako nulový vektor, ale v praxi často nechceme písať, že je tiež ako nula.

Útok vedľa seba – vektorový zákrut vektora na seba:

Pomocou tvorby vektorov môžete skontrolovať kolinearitu triviálnych vektorov a analyzujeme aj ostatné.

Pre väčšinu praktických aplikácií môžete potrebovať trigonometrická tabuľka, zistiť význam dutín.

Nuž, zapálime oheň:

zadok 1

a) Zistite hodnotu vektorovej tvorby vektorov, pretože

b) Nájdite plochu rovnobežníka nakreslenú na vektoroch

rozhodnutie: Nie, toto nie je priateľská milosť, starostlivo som zaplatil víkendové pocty na umývacích staniciach. Pretože bolo rozhodnuté pokračovať v registrácii!

a) Za mysľou, ktorú potrebujete vedieť dovzhin vektor (tvorba vektora). Podľa základného vzorca:

Vidpovid:

Ak sa zjedol o dovzhin, potom sa ukázalo, že druhy majú iba jednu veľkosť.

b) Za mysľou, ktorú potrebujete vedieť oblasť paralelogram založený na vektoroch. Oblasť tohto rovnobežníka je numericky staršia ako vytvorenie vektora:

Vidpovid:

Upozorňujeme, že video o vektorovej vibrácii nie je márne, boli sme naň požiadaní plochejšie postavy Rozmery sú samozrejme štvorcové jednotky.

Vždy sa budete čudovať, čo potrebujete vedieť v zákulisí, a na základe toho formulujeme jasný Potvrdenie. Môžete sa zaseknúť pri doslovnosti, ale listy medzi investormi sú hore a existuje veľká šanca, že sa vrátite na ďalšie preskúmanie. Hoci predpoklad nie je zvlášť napätý - keďže dôkazy sú nesprávne, potom sa rozvinie nepriateľstvo, ktorému osoba nerozumie jednoduchými slovami a / alebo neprenikla do podstaty úlohy. V tomto bode je teraz potrebné vykonávať kontrolu, s najväčšou pravdepodobnosťou aj v oblasti matematiky a iných predmetov.

Kam zmizlo veľké písmeno „en“? V zásade sa dalo dodatočne držať rozhodnutia, ale s metódou krátkej poznámky by som nič neurobil. Dúfam, že všetci chápu, že tým myslia to isté.

Populárny zadok pre nezávislý výkon:

zadok 2

Poznajte oblasť trikutnika na základe vektorov, ako

Vzorec na nájdenie oblasti trikubitu pomocou pridania vektora je uvedený v komentároch pred dátumom. Riešenie a záver hodiny.

V skutočnosti je miestnosť oveľa širšia, môžu si vyhrnúť pančuchy.

Na splnenie ďalších úloh potrebujeme:

Sila vektorových umeleckých vektorov

Orgány tvorby vektorov sa na ne už pozreli, preto ich zaradím do tohto zoznamu.

Pre dostatočné vektory a dostatočný počet spravodlivosti takáto sila:

1) V iných oblastiach informácií úrady tento bod nevnímajú, ale je ešte dôležitejší z praktického hľadiska. Tak nech je.

2) - Moc sa dá nazvať aj inak antikomutativity. Inak sa zdá, že na poradí vektorov záleží.

3) - čokoľvek asociatívne zákony vektorovej praxe. Neustále možno ľahko obviňovať z hraníc tvorby vektorov. Úprimne, čo mám robiť?

4) - samostatné príp distributívny zákony vektorovej praxe. Problémy nie sú ani s otváraním ramien.

Ako ukážku sa pozrime na krátky zadok:

zadok 3

Vediet co

rozhodnutie: Za mozgom musíte poznať podstatu tvorby vektorov. Napíšeme našu miniatúru:

(1) Na základe asociatívnych zákonov zavádzame konštanty za hranicami tvorby vektorov.

(2) Zadajte konštantu medzi modulmi, jej modul má znamienko mínus. Dovzhina môže byť negatívna.

(3) Ďalej to bolo jasnejšie.

Vidpovid:

Nastal čas hádzať drevo do ohňa:

zadok 4

Vypočítajte plochu trikutánneho stromu na základe vektorov

rozhodnutie: Oblasť trikutuly je známa podľa vzorca . Problém je v tom, že samotné vektory „ce“ a „de“ sú reprezentované ako súčet vektorov. Algoritmus je tu štandardný a myslím, že je to dobrý nápad, napríklad č. 3 a lekcia 4 Skalárne vektorové vektory. Pre prehľadnosť je riešenie rozdelené do troch etáp:

1) V prvom kroku je jasné, že vektor tvir cez vektor tvir v podstate virazimo vektor cez vektor. O dovzhiny ešte ani slovo!

(1) Substituované vo vektorových výrazoch.

(2) Vikoristické a distribučné zákony, otvárajúce náruč za vládu množiacich sa bohatých členov.

(3) Vikoristické asociačné zákony, prenášame všetky konštanty za hranice vektorových výtvorov. Ak je zostatok nízky, 2 a 3 je možné zrušiť súčasne.

(4) Po prvé a predovšetkým, zostávajúce prírastky sa rovnajú nule (nulový vektor) trvalého výkonu. Ďalšia dodanku vikoristamo vlastivstvo antikomutatívnosť tvorby vektorov:

(5) Robia sa podobné dodatky.

V dôsledku toho sa vektor objaví cez vektor, čo je potrebné dosiahnuť:

2) V ďalšej fáze zistíme koniec vytvárania vektora, ktorý potrebujeme. Toto je to, čo hádam Príklad 3:

3) Poznáme oblasť shukan trikutnik:

Fázy 2-3 rozhodnutia by sa mohli dokončiť v jednom rade.

Vidpovid:

Pozrite sa bližšie na riadiace roboty, os zadku pre nezávislé ovládanie:

zadok 5

Vediet co

Krátke rozhodnutie A nakoniec, poďme sa rozprávať o lekcii. Človek by sa čudoval, aký rešpekt ste mali k predným zadkom ;-)

Vektorové tvir vektory na súradniciach

, úlohy na ortonormálnom základe, vyjadrené vzorcom:

Vzorec je pomerne jednoduchý: v hornom riadku indexu sú zapísané súradnicové vektory, v druhom a treťom riadku sú súradnice vektorov „uložené“ a v prísnom poradí- Najprv začnem súradnicami vektora „ve“, potom súradnicami vektora „double-ve“. Ak je potrebné vektory vynásobiť v inom poradí, riadky stôp sa obrátia:

Zadok 10

Potvrďte, že vo vesmíre budú dostupné kolineárne vektory:
A)
b)

rozhodnutie: Overenie je založené na jednom z princípov tejto lekcie: keďže vektory sú kolineárne, ich sčítanie vektorov sa rovná nule (nulový vektor): .

a) Poznáme vektor tvir:

Vektory teda nie sú kolineárne.

b) Poznáme vektor tvir:

Vidpovid: a) nie kolineárne; b)

Axis, možno, a všetky hlavné informácie o vytváraní vektorov.

Táto sekcia bude malá, pretože fragmenty poradia, kde sú vektory zmiešané, nie sú bohaté. Takmer všetko bude založené na označení, geometrickom posune a množstve pracovných vzorcov.

Zmiešané pevné vektory – tse tvir trioh vektory:

Náprava tak páchne okolo lokomotívy a kontrolujú, nekontrolujú, keď sa počítajú.

Začínam si spomínať na ten obrázok:

Viznachennya: Zmiešané s tvorbou nekoplanárne vektory, prevzaté z tejto objednávky, volal paralelepiped, vygenerované na týchto vektoroch, so znamienkom „+“, keďže základ je vpravo a znamienkom „–“ ako základ je ľavý.

Vikonaemo malí. Pre nás neviditeľné čiary sú bodkované:

Zamykám sa na stretnutí:

2) Nasnímané vektory v poradí spevu, potom preskupenie vektorov v tvorbe, ako by ste mohli hádať, neprejde bez následkov.

3) Pred komentovaním geometrického posunu upozorním na zrejmú skutočnosť: miešanie pevných vektorov s ČÍSLO: . V pôvodnej literatúre môže byť formátovanie veľmi odlišné, zmes označujem cez a výsledok sa počíta s písmenom „ne“.

Na stretnutia zmiešaná tuhá látka – rovnako ako hranol, vytvorený na vektoroch (obrázok je označený červenými vektormi a čiernymi farebnými čiarami). Toto číslo je staré pre tento rovnobežnosten.

Poznámka : kreslo je schematické.

4) Netrápte sa príliš pojmami orientácia, základ a priestor. Zmysel záverečnej časti vety môže mať znamienko mínus. Jednoducho povedané, zmiešané správy môžu byť negatívne: .

Priamo z hodnoty vyplýva vzorec na výpočet objemu kvádra vytvoreného na vektoroch.

Viznachennya. Vytvorenie vektora vektora a a vektora b je vektor, ktorý je označený symbolom [«, b] (alebo l x b), takže 1) zdvojnásobenie vektora [a, b] je drahšie (p, de y - medzi vektormi a a b (2) vektor [a, b) kolmý na vektory a a b, potom. kolmá na rovinu týchto vektorov; 3) vektor [a, b] narovnania tak, že na konci tohto vektora je viditeľný najkratší obrat z a do b, pretože sa vyskytuje oproti šípke letopočtu (obr. 32). Ryža. 32 Obr. 31 Inak sa zdá, že vektory a, b a [a, b) vytvárajú správne tri vektory. v tvare veľkého, pekného a prostredného prsta pravej ruky. Ak sú vektory a a b kolineárne, budeme brať do úvahy, že [a, b] = 0. Pre vyššie uvedené hodnoty je hodnota vytvorenia vektora číselne vyššia ako plocha Sa rovnobežníka (obr. 33), vytvorené na vektoroch, ktoré sú vynásobené, a a b ako strany: 6.1. Sila vytvorenia vektora 1. Vektorový príjem sa rovná nulovému vektoru a iba ak vezmeme jeden z vektorov na násobenie, ktorý je nula, alebo ak sú vektory kolineárne (buď vektory a a b sú kolineárne, potom je medzi nimi rozdiel, buď 0 alebo 7g) . Dá sa to ľahko odvodiť zo skutočnosti, že ak uvažujeme nulový vektor spolupracujúci s ľubovoľným vektorom, potom mentálnu kolinearitu vektorov a a b možno vypočítať takto: 2. Vektor je antikomutatívny, teda rovnaký. Je pravda, že vektory (a, b) sú identické a kolineárne. Smery týchto vektorov sú rovnobežné, fragmenty z konca vektora [a, b] budú viditeľné krátke odbočenie z a do b, ako je to oproti šípke roka, a od konca vektora [b, a] - za šípkou letopočtu (obr. 34). 3. Vektor tvir má samostatnú silu, kým nie je pridaný 4. Číselný násobiteľ L možno brať ako znak vektorovej kreatívy 6.2. vektorový typ vektorov, dané súradnice Nech sú vektory a a b špecifikované ich súradnicami v základe. Narušiac samostatnú silu tvorby vektorov, poznáme vektorové sčítanie daných súradníc. Zmiešaná televízia. Vektorovú tvorbu súradnicových vektorov zapíšeme (obr. 35): Preto pre vektorovú tvorbu vektorov a a b môžeme od vzorca (3) tento výraz odčítať.Vzorec (4) môžeme zapísať v symbolickom tvare, ktorý je ľahko zapamätateľný, pretože sa rýchlo stane dôsledkom 3. rádu. : Umiestnite tento riadok za prvky prvého radu, odstráňte ho (4). aplikujte to. 1. Nájdite oblasť rovnobežníka vygenerovaného na Shukanových vektoroch, oblasť Toma je známa = hviezdy 2. Nájdite oblasť trikutánneho (obr. 36). Je zrejmé, že plocha b"d trikutánnej DPH je viac ako polovica plochy S rovnobežníka O AC B. Výpočtová vektorová pevná látka (a, b| vektory a = OA a b = oЪ, je odvoditeľná Zvidsi Zauvazhenya. Vektorové teleso nie je asociatívne, potom je žiarlivosť (a, b ),c) = [a, |b,c)) v začiatočnej vete nesprávna Napríklad s a = ss j môžeme § 7. Miešanie sčítania vektorov Majme tri vektory a, b a c. [a, 1>] Vynásobme y skalár vektorom 3: (k b), c) Číslo ([a, b], e) sa nazýva zmiešaný súčin vektorov. a, b, c i je označené symbolom (a, 1), e) 7.1 Geometrický význam zmiešaného výtvoru Pridáme vektory a, b a z bodov, ktoré vyšli (obr. 37) Keďže všetky body O, A , B, C ležia v rovnakej rovine (vektory a, b a c sa v tomto prípade nazývajú koplanárne), potom zmes tuhá látka ([a, b], c) = 0. Vyplýva to z toho, že vektor [a , b| je kolmé na rovinu, v ktorej ležia vektory a a 1, a preto vektor c./ t okulárov O, A, B, C neleží v rovnakej rovine (vektory a, b a z nie sú koplanárne), budú na okrajoch OA, OB a OS rovnobežnostena (obr. 38 a). Pre hodnoty vytvorenia vektora máme (a, b) = So, kde So je plocha rovnobežníka OADB a z je jeden vektor kolmý na vektory a a b a taký, že trojnásobok a, b, c majú teda pravdu. vektory a, b a s majú tvar veľkého, vulgárneho a prostredníka pravej ruky (obr. 38 b). Vynásobením problematických častí zostávajúcich rovníc vpravo skalárnym vektorom sa odstráni, že vektor je sčítaním vektorov daných súradnicami. Zmiešaná televízia. Číslo pg sa rovná výške h vygenerovaného rovnobežnostena, pričom znamienko „+“ je medzi vektormi so stranami a so stranami (trojité a, b, c - vpravo) a so znamienkom „-“. , čo je hlúpe (trojité a, b , s - vľavo), takže Tim sám zmiešaním sčítania vektorov a, b a z tradičného V rovnobežnostenu vygeneroval na týchto vektoroch ako na hranách, ako je trojité a, b, c - vpravo, i -V, ako trojité a, b, s – liva. Vychádzajúc z geometrického významu zmiešaného stvorenia, môžeme zostaviť vzorec, ktorý vynásobením rovnakých vektorov a, b a v akomkoľvek inom poradí potom odstránime buď +7 alebo -K. Znak Virob Obr. 38 informácií závisí len od toho, že sa vytvoria tri vektory, ktoré sa násobia - doprava alebo doľava. Ak vektory a, b tvoria pravú trojku, potom trojice b, c, a a c, a, b budú tiež správne. Tá istá hodina má všetky tri tri b, a, h; a, s, b i s, b, a – živ. Tim samotný, (a,b, c) = (b,c, a) = (c,a,b) = -(b,a,c) = -(a,c,b) = -(c,b A). Ešte raz zdôraznime, že zmiešanie dvoch vektorov je jedna nula len vtedy, ak sú vektory a, b, s vynásobené: (a, b, s koplanárne) 7.2. Zmiešajte teleso v súradniciach vektorov a, b, iz dané ich súradnicami v báze i, j, k: a = (x\,y\,z]), b=(x2,y2>z2), c = (x3, uz, 23). Poznáme výraz tohto košatého výtvoru (a, b, h). Môže existovať zmes troch vektorov určených súradnicami v báze i, J až po začiatok tretieho rádu, ktorých rady sú tvorené podľa súradníc prvého, druhého a tretieho z vektorov, ktoré sú znásobené. Je potrebné, aby dostatočná mentálna koplanarita vektorov a y\, Z|), b = (хъ У2. 22), с = (жз, з, 23) bola zapísaná tak, У | z, ag2 y2 -2 = 0. Uplatnená univerzita. Skontrolujte, či ide o koplanárne vektory „ = (7,4,6), b = (2, 1,1), c = (19, II, 17). Vektory, na ktoré sa pozeráme, budú koplanárne alebo nekoplanárne, v závislosti od toho, že sa rovnajú nule a ani počiatku prvkov prvého riadku, môžeme odstrániť D = 7- 6- 4- 15 + 6 -3 = 0^- vektory n, b, s koplanárne . 7.3. Podriadené vektorové teleso Podriadené vektorové teleso [a, [b, c]] je vektor kolmý na vektory a a [b, c]. Preto leží v rovine vektorov b a c a môže sa týmito vektormi rozložiť. Dá sa ukázať, že platí vzorec [a, [!>, c]] = b(a, e) - c(a, b). Vpravo 1. Tri vektory AB = c, F? = asi SA = b slúžia ako strany trikuputnika. Vyjadrite cez a, b a vektory, ktoré sa zhodujú s mediánmi AM, DN, CP trikutánneho. 2. Podľa čoho sú vektory p a q spojené, aby sa medzi ne rozdelil vektor p + q? Prenáša sa, že všetky tri vektory sú prinesené do klasu. 3. Vypočítajte polovicu uhlopriečok rovnobežníka nakreslených na vektoroch a = 5p + 2q a b = p - 3q, pretože je zrejmé, že |p| = 2v/2, | q | = 3H-(p7ci) = f. 4. Po vyznačení strán kosoštvorca, ktoré vychádzajú z vrchola rohu, cez a a b sa uistite, že uhlopriečky kosoštvorca sú navzájom kolmé. 5. Vypočítajte skalárny súčet vektorov a = 4i + 7j + 3k a b = 31 - 5j + k. 6. Nájdite jednotkový vektor a0, rovnobežný s vektorom a = (6, 7, -6). 7. Nájdite priemet vektora a = l + j-kHa vektor b = 21 - j - 3k. 8. Nájdite kosínus vektora medzi vektormi IS «w, ako napríklad A (-4,0,4), B (-1,6,7), C (1,10,9). 9. Nájdite jednotkový vektor p°, kolmý na vektor a = (3, 6, 8) a os Ox. 10. Vypočítajte sínus štvorca medzi uhlopriečkami rovnobežníka vygenerovaného na vektoroch a = 2i+J-k, b=i-3j + k ako na stranách. Vypočítajte výšku h kvádra vygenerovaného na vektoroch a = 31 + 2j - 5k, b = i-j + 4knc = i-3j + k na základe rovnobežníka vygenerovaného na vektoroch a a I). Typy

Viznachennya. Vytvorenie vektora a (násobku) na kolineárny vektor (násobič) sa nazýva tretí vektor z (tvir), čo bude ďalší krok:

1) tento modul je numericky starší ako rovina rovnobežníka na obr. 155) na základe vektorov, ktoré sú priamo kolmé na rovinu uhádnutého rovnobežníka;

3) v tomto prípade sa vektory vyberajú priamo (z dvoch možných) tak, aby vektory tvorili správnu sústavu (§ 110).

Označenie: buď

Pridané k dátumu. Keďže vektory sú kolineárne, potom sú čísla dôležitými (mentálne) rovnobežníkmi, a preto im treba priradiť nulovú plochu. Preto sa vektorové sčítanie kolineárnych vektorov považuje za rovné nulovému vektoru.

Fragmenty možno priradiť k nulovému vektoru akýmkoľvek priamym spôsobom, aby neboli v rozpore s bodmi 2 a 3.

Rešpekt 1. V pojme „vektorová pevnosť“ prvé slovo označuje tie, ktorých výsledkom je vektor (na rozdiel od skalárneho tvorenia; rovná sa § 104, ohľad 1).

Aplikácia 1. Zistite vektorový vektor, hlavné vektory pravého súradnicového systému (obr. 156).

1. Fragmenty dvoch hlavných vektorov sa rovnajú jednotkám mierky, potom sa plocha rovnobežníka (štvorca) číselne rovná jednotkám. Tiež vektorový modul je staršia jednotka.

2. Fragmenty sú kolmé na rovinu - os, potom je hľadaná vektorová pevná látka vektor kolineárny k vektoru do; Pretože to bolí smrad modulu 1, hľadanie vektorových prídavkov je buď k alebo -k.

3. Z týchto dvoch možných vektorov je potrebné vybrať prvý, aby vektory vytvorili systém vpravo (a vektory vľavo).

Príklad 2. Poznajte vektor tvir

rozhodnutie. Ako napríklad 1, môžeme povedať, že vektor je rovnaký ako k alebo -k. Teraz však musíte vybrať -k, aby vektory nastavili systém doprava (a vektory doľava). Otje,

Príklad 3. Vektory sú nakreslené presne na rovnakej úrovni ako 80 a 50 cm a uhol 30°. Berúc dovzhini meter ako jeden, zistite dovzhin tvorby vektorov

rozhodnutie. Oblasť rovnobežníka vytvoreného na vektoroch je stará. Dovzhina hľadanej tvorby vektorov je stará.

Príklad 4. Zistite dovzhin vektorovej tvorby týchto samotných vektorov, pričom dovzhin centimeter ako jeden.

rozhodnutie. Fragmenty oblasti paralelogramu generované vektormi sú staré ako dovzhina vektora dobutu ako 2000 divas.

Zo zarovnania aplikácií 3 a 4 je zrejmé, že dovzhin vektora leží ako výsledok dovzhin faktorov a ako výsledok výberu jednotky dovzhin.

Fyzický zmysel pre tvorbu vektorov. Z číselných fyzikálnych veličín, ktoré sú reprezentované vektorovou tvorbou, uvažujme iba moment sily.

Bodom hlásenej sily nech je A. Moment sily do bodu O nazývame vektorové teleso Fragmenty modulu tohto vytvorenia vektora sú číselne staršie ako plochý rovnobežník (obr. 157), potom modul momentu je vyššia ako dodatočná hodnota dosadenia za výšku, potom sila, vynásobená stojanom od bodu O k priamke, Aký druh sily je tam?

Mechanizmus si uvedomuje, že z rovnováhy pevného telesa je potrebné rovnať sa nule ako súčtu vektorov, ktorými sú sily pôsobiace na teleso, a tiež súčtu momentov síl. V tomto prípade, ak sú všetky sily rovnobežné s rovnakou rovinou, záhyb vektorov, ktoré predstavujú momenty, môže byť nahradený pridanými a odstránenými modulmi. Bez dostatočných priamych síl je takáto výmena nemožná. Je zrejmé, do akej miery je vektorové číslo definované ako samotný vektor a nie ako číslo.

Vektorový vitvir- toto je pseudovektor kolmý na rovinu generovaný dvoma násobiteľmi, ktorý je výsledkom binárnej operácie „násobenia vektorov“ na vektoroch v triviálnom euklidovskom priestore. Vektorový vektor nemá silu komutativity a asociatívnosti (a antikomutácie) a na rozdiel od skalárneho vytvárania vektorov je vektorom. Široko používaný v rôznych technických a fyzikálnych aplikáciách. Napríklad moment hybnosti a Lorentzova sila sú matematicky zapísané ako vektorový súčin. Pridanie vektora je hnedé, aby „rozvibrovalo“ kolmosť vektorov – vektorový modul vytvorí dva vektory pomocou rovnakého sčítania modulov, ak sú kolmé, a zmení sa na nulu, ak sú vektory paralelné alebo antiparalelné.

To znamená, že vektorové teleso je možné rôznymi spôsobmi a teoreticky pre priestor ľubovoľného rozmeru n môžete vypočítať teleso z n-1 vektorov, pričom od toho vášho odčítate jeden vektor kolmý na všetky z nich. Ak je teleso prepojené s netriviálnymi binárnymi výtvormi s vektorovými výsledkami, potom je tradičné vektorové teleso definované iba v triviálnych a sedemrozmerných priestoroch. Výsledok tvorby vektora, ako aj skalárneho, leží v rámci metrík euklidovského priestoru.

Okrem vzorca na výpočet súradníc vektorov skalárneho systému v trojrozmernom priamočiarom súradnicovom systéme musí byť vzorec pre vektorový súčin založený na orientácii priamočiareho súradnicového systému alebo inak „chiralite“.

Hodnota:
Vektorové pridanie vektora a k vektoru b v priestore R 3 sa nazýva vektor c, čo naznačuje nadchádzajúce výsledky:
dovzhin vektor c dovzhinu dovzhena vektory a a b sínusom rezu φ medzi nimi:
|c|=|a||b|sin φ;
vektor c ortogonálny ku kožnému vektoru c vektory a a b;
vektor c je rektifikovaný tak, že tri vektory abc sú pravotočivé;
Pre každý priestor R7 je potrebná asociativita troch vektorov a, b, c.
Určené:
c===a × b

Ryža. 1. Oblasť rovnobežníka je staršia ako vektorový modul

Geometrická sila vektorového umenia:
Nevyhnutná a dostatočná mentálna kolinearita dvoch nenulových vektorov sa rovná nule ich tvorby vektorov.

Vektorový kreatívny modul staroveká oblasť S rovnobežník, vytvorený redukciou na frontálne vektory aі b(Div. Obr. 1).

Yakshcho e- jednoduchý vektor, ortogonálny vektor aі b a výbery tak, že tri a,b,e- správne a S- oblasť rovnobežníka nakreslená na nich (smerovaná na predný klas), potom pre vytvorenie vektora platí nasledujúci vzorec:
=S e

Obr.2. Objem rovnobežnostena s vikoristanom vektorových a skalárnych vektorov; Bodkované čiary zobrazujú projekcie vektora c na a × b a vektora a na b × c, prvý riadok je umiestnenie skalárnych výtvorov

Yakshcho c- aký druh vektora, π - nech je to plochosť, pomstiť sa tomuto vektoru, e- jeden vektor, ktorý leží blízko roviny π і ortogonálne k c,g- jeden vektor, kolmý na rovinu π a rektifikácie tak, že tri vektory EKGє správne, potom pre každého, kto leží pri námestí π vektor a vzorec je správny:
=Pr e a |c|g
de Pr e projekcia vektora e na a
|c|-modul vektora z

S vikoristanom vektorových a skalárnych výtvorov je možné virahuvat rovnobežnosten vytvorený redukciou na vektory klasu. a, bі c. Takáto kombinácia troch vektorov sa nazýva zmiešaná.
V=|a (b×c)|
Malý ukazuje, že to možno nájsť dvoma spôsobmi: geometrický výsledok sa zachová pri nahradení „skalárnych“ a „vektorových“ výtvorov:
V=a×b c=a b×c

Hodnota vektorového súčinu leží v sínusu kružnice medzi primárnymi vektormi, takže vektorové teleso možno považovať za úroveň kolmosti vektorov, rovnako ako skalárne teleso možno považovať za úroveň rovnobežnosti. Pridanie vektora dvoch jednotlivých vektorov je vyššie ako 1 (jeden vektor), ak sú cob vektory kolmé, a vyššie ako 0 (nulový vektor), ak sú vektory paralelné alebo antiparalelné.

Viraz pre tvorbu vektorov v karteziánskych súradniciach
Existujú dva vektory aі b definované ich pravouhlými karteziánskymi súradnicami, alebo presnejšie, reprezentované na ortonormálnom základe
a = (a x, a y, az)
b = (b x, b y, b z)
a súradnicový systém je správny, potom vyzerá jeho vektorové teleso
=(a y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
Aby ste si zapamätali tento vzorec:
i = ∑ε ijk a j b k
de ε ijk- symbol Levi-Chivity.